[Deep Learning 1] 퍼셉트론
퍼셉트론의 등장과 1차 암흑기
최초의 인공 신경망(ANN; Artificial Neural Network)은 1943년 신경 생리학자인 매컬러(McCulloch)와 수학자 피츠(Pitts)에 의해 고안되었다.

이 ANN 모델은 활성/비활성 상태의 이진 뉴런(binary neuron)으로 구성되는데, 마치 실제 우리 몸의 뉴런과 같이 전달된 신호가 특정 임계치를 넘어야 신호가 발화되는 구조이다.
이후 1956년 신경 생물학자인 로젠블랫(Rosenblatt)이 ANN이 스스로 문제에 맞춰 학습하는 모델인 퍼셉트론(perceptron)을 고안해냈다.
로젠블랫과 같은 연결주의 학파들은 뉴런를 모방함으로써 데이터로부터 스스로 지능을 만들 수 있을 것이라고 믿었다. 하지만…
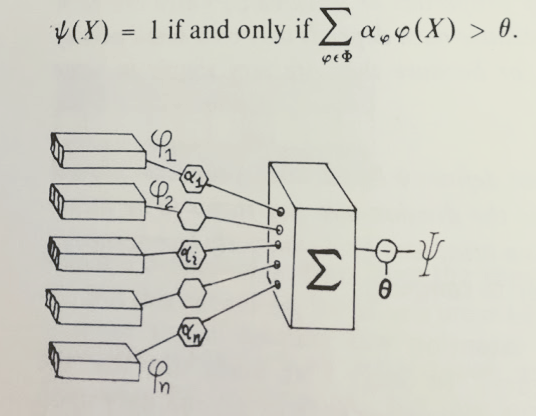
반대파였던 기호주의 학파의 민스키(Minsky)와 페퍼트(Papert)는 퍼셉트론이 비선형 문제는 풀 수 없다는 한계를 입증하면서 퍼셉트론의 인기는 식어가고 연구도 더뎌졌다.
이를 AI 학계에서는 ‘1차 암흑기(겨울, 1974-1980)’라고 부른다. 이 비선형 문제에 대한 해결책은 이번 장에서 후술하겠다.
퍼셉트론이 뭐길래?
퍼셉트론은 우리 뇌의 기본 단위인 뉴런과 같이, 다수의 신호를 입력으로 받아 하나의 신호를 출력하는 신경망을 말한다.
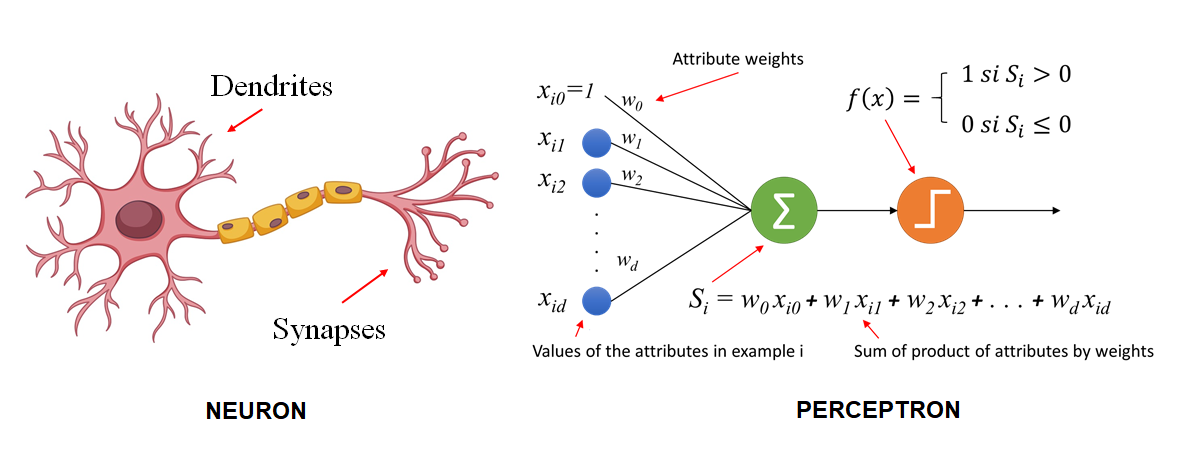
뇌를 구성하는 뉴런은 수상돌기(dendrites)로 들어오는 신호를 세포체(cell body)에 모았다가 그것이 특정 임계치를 넘으면 이 신호를 축삭돌기(axon)의 말단에 있는 시냅스(synapse)로 발화(trigger)한다. 즉 뉴런이 활성화(activated)된 것이다.
이 신호를 펄스 혹은 스파이크 단위로 발생되는데, 해당 신호의 전달이 반복될 경우 시냅스 간의 연결이 강화되며 구조가 변하게 되는데, 이를 가소성(plasticity)이라고 한다.
이 구조를 본따 만든 것이 퍼셉트론으로, 벡터인 입력(x)과 역시 벡터인 가중치(w)를 곱하여 다 더한 후, 그 합이 특정 임계치를 넘으면 1을 출력하고, 그렇지 않다면 0을 출력하는 구조이다.

이때 식을 보면 시그마(합)이 가중치 벡터의 전치(w transpose)와 신호 벡터(x)의 곱에 편향(b)을 더한 가중합산으로 표현되며, 이 값이 0보다 크면 1이 출력되는 계단 함수(혹은 활성함수)에 집어 넣어 결과 y를 도출하는 방식이다.
즉 퍼셉트론은 신호 벡터 x만 들어온다면, 가중치 벡터 w와 편향 b의 값만을 조정함으로써 결과를 바꿀 수 있는데, 이것이 퍼셉트론이 스스로 학습하는 방식인 것이다.
퍼셉트론으로 AND, NAND, OR 게이트 구현
바로 위에서 말했듯 w와 b값만 만져주면 게이트가 바뀐다. 직접 확인해보자.
import numpy as np
def AND(x1, x2):
x = np.array([x1,x2])
w = np.array([0.5,0.5])
b = -0.7
tmp = np.sum(w*x) + b
if tmp <= 0:
return 0
else:
return 1
def NAND(x1, x2):
x = np.array([x1, x2])
w = np.array([-0.5, -0.5]) # AND와 가중치(w와 b)만 다름
b = 0.7
tmp = np.sum(w*x) + b
if tmp <= 0:
return 0
else:
return 1
def OR(x1, x2):
x = np.array([x1, x2])
w = np.array([0.5, 0.5]) # AND와 가중치(w와 b)만 다름
b = -0.2
tmp = np.sum(w*x) + b
if tmp <= 0:
return 0
else:
return 1
실로 간단하다. 이해가 안된다면 직접 x값에 0과 1을 넣으면서 진리표를 만들어보자.
다층 퍼셉트론을 활용한 비선형 문제 해결
아까 언급한 1차 암흑기의 비선형 문제는 무엇이냐? 바로 XOR 게이트에 대한 문제이다.
이 이미지에 아주 잘 표현되어 있는데, 앞서 만든 AND와 NAND 및 OR는 그래프(좌표평면) 상에서 선 하나로 간단하게 영역을 그을 수 있다. 그런데 XOR(exclusive or: 같으면 0, 다르면 1)는 어떻게 그을 수 있을까?
이 문제에 대한 지적에서 퍼셉트론의 인기는 식어갔다. 그러나 방법은 있었다. 선을 직선(선형)이 아닌 곡선(비선형)으로 그으면 되는 문제이기 때문이다.
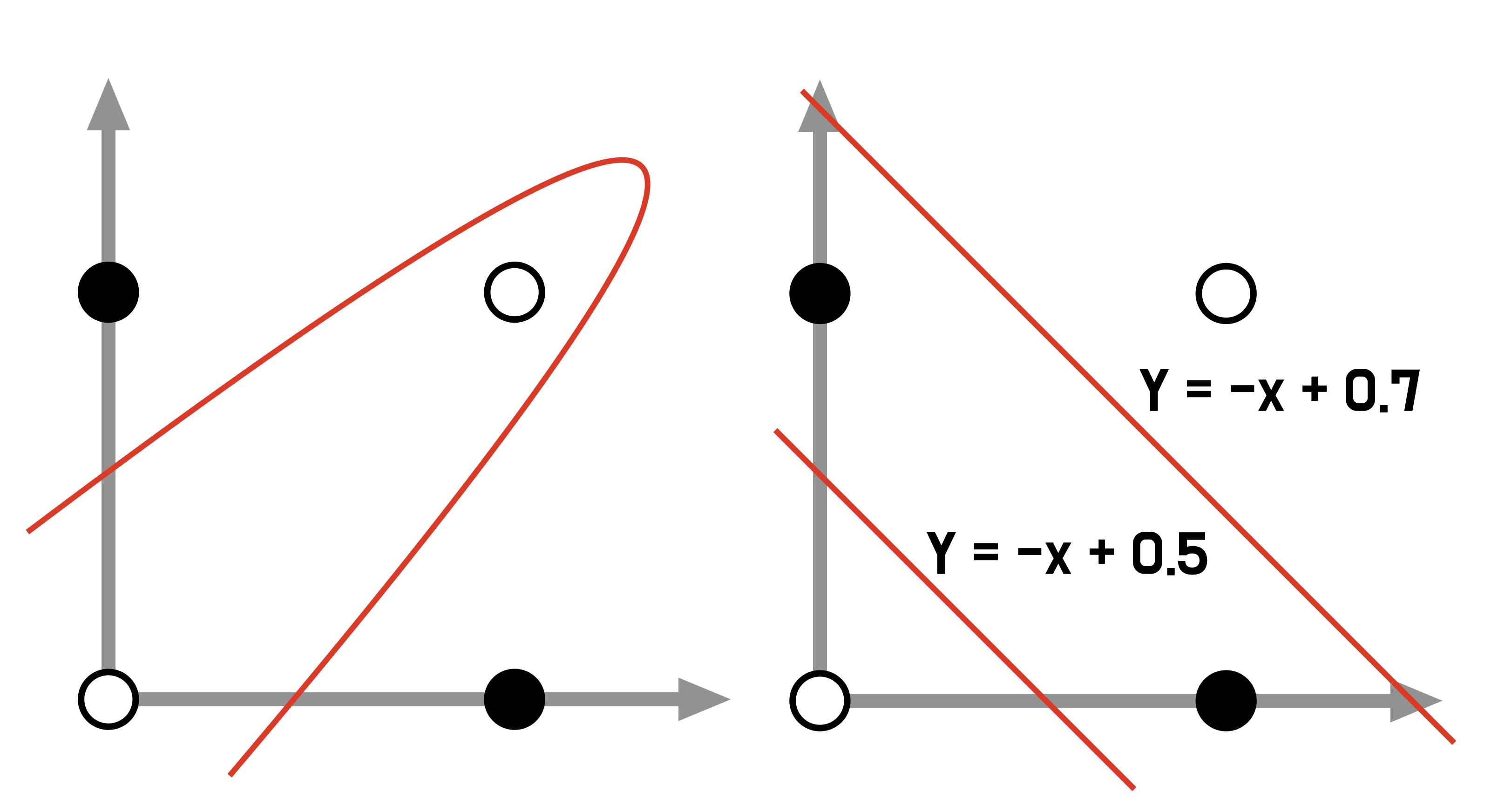
다음과 같이(좌) 포물선(비선형)으로 영역을 그으면 XOR 문제가 간단히 풀린다. 혹은 선을 두 개 긋거나(우), 두 영역을 AND 연산함으로써도 해결할 수 있다.
이것이 다층 퍼셉트론(multi-layer perceptron)이다. 종전의 단층 퍼셉트론과 달리, 신호를 처리하는 층을 늘림으로써 더 다양한 것을 표현할 수 있게 된다.
XOR은 사실 NAND와 OR의 AND연산으로 해결된다. (NAND를 통해 모든 게이트를 구현할 수도 있다!) 코드를 통해 확인해보자.
# 앞선 AND, NAND, OR 코드 아래에 덧붙이면 된다
def XOR(x1, x2):
s1 = NAND(x1, x2)
s2 = OR(x1, x2)
y = AND(s1, s2)
return y
진리표를 계산해보니 정말 XOR 연산이 가능함을 알 수 있다. 즉 퍼셉트론으로 XOR 연산을 구현할 수 있는 것이고, 확대해석하자면(?) 퍼셉트론으로 모든 게이트를 구현 가능, 즉 퍼셉트론만으로 컴퓨터를 만들 수도 있다는 말이 된다.
정리하자면, 퍼셉트론은 층을 쌓을 수록 더 다양한 비선형적 표현을 할 수 있고, 곧 컴퓨터가 수행하는 처리도 모두 표현할 수 있다.
출처: [밑바닥부터 시작하는 딥러닝 Chapter 2]
참고: [Do it! 딥러닝 교과서 p.23~37]