[Deep Learning 10] OUTTA 딥러닝 basic반 1~3강
초반 내용은 직전에 공부했던 ‘밑바닥부터 시작하는 딥러닝’ 책의 내용과 상당히 유사해서 이론을 이해하는 데 막히는 부분은 없었다.
대신 생각보다 과제가 양이 많아서 따라하는데도 두 시간 이상씩 걸렸음.. 특히 2강..
겹치는 내용이나 내가 이미 포스팅한 내용이 많아서 이번엔 다루지 못했던 부분만 간략히 다뤄보겠다!
이론적으로 보충할 내용
일단 이 많은 내용을 정리해서 엮어준 OUTTA 부트캠프 운영진분들이 존경스럽다. 이론 내용도 그렇고, 특히 뒤에서 다룰 ipynb 내용이 정말 방대하다. 이걸 어떻게 다 쓰신거지? 심지어 수식적으로 엄밀하다.
최소 제곱 추정량
최소 제곱법(Least Squared Method)에서 RSS(잔차제곱합)으로 손실 함수(loss function)를 정의하면 다음과 같다.
\[L(m, b; (x_n, y_n^{(true)})_{n=0}^{N-1})=\sum_{n=0}^{N-1}(y_n^{(true)}-F(m, b; x_n))^2\]기울기 m과 y절편 b에 대하여, 손실 함수 L은 실제값에서 산출값(예측값)을 뺀 것의 제곱합으로 계산된다는 뜻이다. 여기까진 별로 어렵지 않다.
\[m^*, b^*=argmin_{m, b\in R}L\]이때 손실 함수를 최소로 하는 HyperParameter m스타와 b스타를 최소 제곱 추정량(LSE; Least Squared Estimator)이라 부른다.
이 모델이 선형 모델이라 선형성(linearity)을 충족한다고 가정하자. 그렇다면 y=mx+b라는 산점도 상의 적합선(best fit line)을 그릴 수 있다.
\[\begin{align} L &=\sum_{n=0}^{N-1}(y_n-(mx_n+b))^2 \\ &=\sum_{n=0}^{N-1}(m^2x_n^2+b^2+y_n^2+2bmx_n-2mx_ny_n-2by_n) \end{align}\]여기서 손실 함수 L을 m과 b에 대해 편미분하면
\[\frac{\partial L(m,b)}{\partial m}=\sum_{n=0}^{N-1}(2mx_n^2+2bx_n-2x_ny_n)=0 \cdots (1)\] \[\frac{\partial L(m,b)}{\partial b}=\sum_{n=0}^{N-1}(2b+2mx_n-2y_n)=0 \cdots (2)\]이렇게 나오며, 각각이 0이 될 때 RSS값이 최소가 되는, 즉 최소 제곱 추정량이 될 것이다. (실제로는 0이 안될 수 있다. 그러나 이렇게 계산하면 근사는 가능하다.)
식(1)을 m에 대해 정리하면
\[m\sum_{n=0}^{N-1}x_n^2+b\sum_{n=0}^{N-1}x_n=\sum_{n=0}^{N-1}x_ny_n \cdots (3)\]이고 식(2)를 b에 대해 정리하면
\[2bN+2m\sum_{n=0}^{N-1}x_n-2\sum_{n=0}^{N-1}y_n=0\] \[b=\frac{\sum_{n=0}^{N-1}y_n-m\sum_{n=0}^{N-1}x_n}{N} \cdots (4)\]이다. 식(4)을 식(3)에 대입하여 정리해주면
\[m\sum_{n=0}^{N-1}x_n^2+\frac{1}{N}(\sum_{n=0}^{N-1}x_n\sum_{n=0}^{N-1}y_n-m(\sum_{n=0}^{N-1}x_n)^2)=\sum_{n=0}^{N-1}x_ny_n\]m으로 묶어주면
\[m(\sum_{n=0}^{N-1}x_n^2-\frac{1}{N}(\sum_{n=0}^{N-1}x_n)^2)+\frac{1}{N}(\sum_{n=0}^{N-1}x_n\sum_{n=0}^{N-1}y_n)=\sum_{n=0}^{N-1}x_ny_n\]에서 m에 대한 식으로 정리하면
\[\textcolor{red}{m^*}=\frac{\sum_{n=0}^{N-1}x_ny_n-\frac{1}{N}(\sum_{n=0}^{N-1}x_n\sum_{n=0}^{N-1}y_n)}{\sum_{n=0}^{N-1}x_n^2-\frac{1}{N}(\sum_{n=0}^{N-1}x_n)^2}\]이 된다. 보기 쉽게 나타내자면
\[\textcolor{red}{m^*}=\frac{\sum{xy}-\frac{1}{N}(\sum{x}\sum{y})}{\sum{x^2}-\frac{1}{N}(\sum{x})^2}\]이고 b*는 식(2)의 양변을 2N으로 나누었을 때
\[\textcolor{blue}{b^*}=\bar{y}-\textcolor{red}{m^*}\bar{x}\]와 같이 놓을 수 있다. 이제 이 식과 동일하게 파이썬 코드를 짜면 된다! 참고로 이 식은 MSE에도 적용 가능하다. (RSS를 N으로 나눈 게 MSE이기 때문)
공분산과 분산을 사용한 최소제곱추정량 계산
앞서 사용한 m*의 식을 더 간단히 바꿔볼 것이다. 이 변환의 핵심은 아래의 식이다.
\[\frac{1}{N}\sum_{n=0}^{N-1}x_i\sum_{n=0}^{N-1}y_i=N\bar{x}\bar{y}=\sum_{n=0}^{N-1}\bar{x}\bar{y}=\sum_{n=0}^{N-1}x_i\bar{y}=\sum_{n=0}^{N-1}\bar{x}y_i\]이해가 되는가? x bar(x의 평균)과 y bar(y의 평균)이 상수 계수처럼 취급되기에 마음대로 시그마를 붙였다 뗐다 할 수 있는 것이다. 따라서 m*의 분자는
\[\begin{align} \sum{xy}-\frac{1}{N}(\sum{x}\sum{y}) &=\sum{xy}-\sum\bar{x}\bar{y} \\ &= \sum{xy}-\sum\bar{x}\bar{y} + (2\sum\bar{x}\bar{y}-\sum\bar{x}y-\sum{x}\bar{y}) \\ &= \sum(xy-\bar{x}\bar{y}+2\bar{x}\bar{y}-\bar{x}y-x\bar{y}) \\ &= \sum(xy+\bar{x}\bar{y}-\bar{x}y-x\bar{y}) \\ &= \sum(x-\bar{x})(y-\bar{y}) \\ &= \textcolor{green}{N\times Cov(x, y)} \end{align}\]로 x와 y의 공분산꼴이 된다! 같은 방식으로 m*의 분모는
\[\begin{align} \sum{x^2}-\frac{1}{N}(\sum{x})^2 &= \sum{x^2}-N\bar{x}^2 \\ &= \sum{x^2}-N(\bar{x}^2+2\bar{x}x-2\bar{x}^2) \\ &= \sum(x^2-2\bar{x}x+\bar{x}^2) \\ &= \sum(x-\bar{x})^2 \\ &= \textcolor{green}{N\times Var(x)} \end{align}\]x의 분산꼴이 된다! 따라서 둘을 정리하여 약분하면
\[\textcolor{red}{m^*}=\frac{\sum(x-\bar{x})(y-\bar{y})}{\sum(x-\bar{x})^2}= \textcolor{red}{\frac{Cov(x,y)}{Var(x)}}\]이다. b*는 마찬가지로
\[\textcolor{blue}{b^*}=\bar{y}-\textcolor{red}{m^*}\bar{x}\]이다. 최소제곱추정량(LSE) m*가 공분산을 분산으로 나눈 꼴이 되는 이유는, 두 변수 X와 Y의 기울기(선형 관계)는 얼마나 같은 방향으로 움직이는 경향이 있는지에 대한 지표이기 때문이다.
공분산은 두 변수가 같은 방향이면 양수, 다른 방향이면 음수를 띠므로 공분산을 포함하여 기울기를 찾을 수 있게 된다.
경사하강법 수식(-붙이는 이유)
경사하강법에서 각 가중치(weight) w에 대한 갱신은 다음 식으로 이뤄진다.
\[w_{new}=w_{old} \textcolor{red}{-}\delta \cdot \frac{dL}{dw}|_{w=w_{old}}\]이때 (편)미분계수 dL/dw를 학습률(delta)과 곱하여 기존 값에서 빼주는데, 그 이유는 기울기가 양수이면 반대 방향인 좌측으로 가중치가 이동해야하기 때문이다.
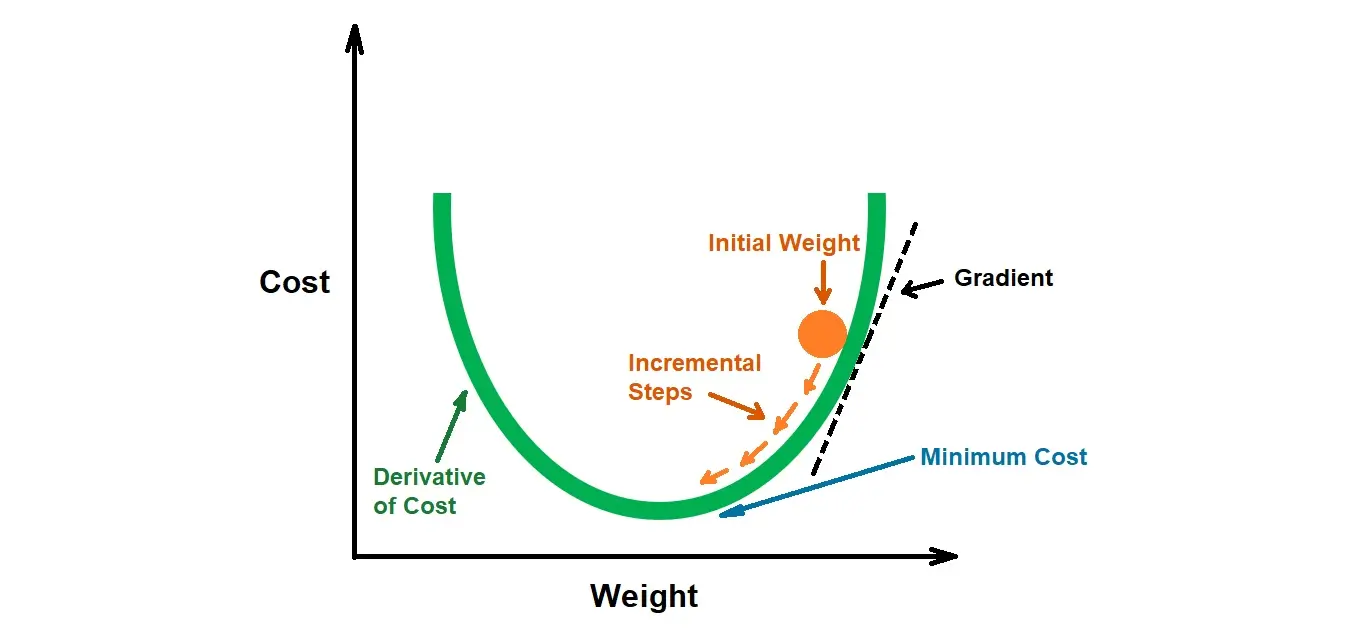
처음엔 무슨 말인가 했는데 조금만 생각하면 너무 당연한 말이었다. 반대로 기울기가 음수면 반대 방향인 우측으로 이동해야 손실 함수 값이 더 작아지게 된다.
전처리의 중요성
인간과 달리 컴퓨터는 주어진 수치의 단위와 크기 차이를 능동적으로 가려내지 못한다. 즉 80cm와 100cm는 인간이 보기엔 거기서 거기의 차이이지만, 컴퓨터 입장에서는 아주 상이한 값으로 인식될 수 있다는 것.
이것이 단위가 달라지거나, 둘 이상의 다른 단위 데이터끼리의 산점도(예: 일자(자연수, 단위: 일)에 따른 온도(실수, 단위: 섭씨))를 나타낼 때 왜곡을 일으킬 수 있다. 따라서 데이터 전처리를 해주어야 한다.
크게 두 가지인데, 최소-최대 정규화와 Z 정규화가 있다. 최소-최대 정규화는 모든 수치를 0과 1사이의 값으로 변환하는 것인데, 최솟값은 0, 최댓값은 1로 변환된다.
\[x'=\frac{x-min(Data)}{max(Data)-min(Data)}\]Z 정규화는 확률과 통계때부터 주구장창 배우는 표준정규분포곡선 Z를 따르는 정규화다. 각 수치에서 평균을 빼준 뒤 표준편차로 나눠준다.
\[Z=\frac{X-\mu}{\sigma}\]둘다 알고있는 내용이지만, 새삼 정규화가 딥러닝 과정에서 꼭 필요한 전처리 과정이라는 생각이 들어서 다시 한 번 강조해 보았다.
실습에서 특기할만한 내용
PyTorch 사용
코랩에서 딥러닝 학습을 진행할 때 자주 사용되는 라이브러리로 PyTorch(파이토치)가 있다. 기존에 TensorFlow는 사용해 보았지만, 파이토치를 이번 실습을 통해 다루게 되어서 기쁘다.
파이토치는 다음과 같이 임포트한다.
import torch
PyTorch는 GPU의 병렬 처리를 사용하기 때문에 본격적으로 활용하기 위해선 CPU가 아닌 GPU, 혹은 CUDA로 설정하여 사용하여야한다.
PyTorch는 텐서(Tensor)를 기본 자료형으로 사용하는데, numpy.ndarray와 비슷한 느낌이다. 대신 matplotlib을 사용하려면 텐서를 numpy.ndarray로 변환하여 처리하는 것이 빠르다는 점에 유의하자.
matmul연산과 einsum연산
matmul과 einsum 모두 내적 및 행렬곱을 위한 PyTorch의 연산처리 방식이다. 다만 그 표기가 조금 다른데 확인해보자. 먼저 1, 2차원 텐서의 matmul 연산은 다음과 같다.
x = tc.tensor([1.0, 2.0])
y = tc.tensor([-3.0, -4.0])
tc.matmul(x, y)
# 혹은 x @ y로도 계산 가능
# 결과: tensor(-11.)
1차원 텐서에서는 내적으로 계산된다. 이때 @로 간단히 matmul 연산을 시킬 수 있다.
a = tc.tensor([[1, 0], [0, 1], [2, 1], [3, 4]])
b = tc.tensor([[4, 1, 5], [2, 2, 6]])
a @ b# tc.matmul(a, b)
# 결과:
# tensor([[ 4, 1, 5],
# [ 2, 2, 6],
# [10, 4, 16],
# [20, 11, 39]])
2차원 텐서에선 행렬곱으로 계산된다. 3차원 이상에서는 2차원 행렬을 나머지 N-2 차원으로 쪼개 각각의 행렬곱을 계산한 후 다시 합치는 과정을 거친다. 브로드캐스팅 연산도 자연스럽게 수행된다.
# A는 크기가 (4, 2, 3)인 3차원 텐서
A1 = tc.arange(2*3).reshape((2,3))
A = tc.stack([A1, A1+2, A1+4, A1+6])
# B는 크기가 (4, 3, 3)인 3차원 텐서
B1 = tc.arange(3*3).reshape((3,3))
B = tc.stack([B1, B1+2, B1+4, B1+6])
print(tc.matmul(A, B))
# 결과:
# tensor([[[ 15, 18, 21],
# [ 42, 54, 66]],
# [[ 51, 60, 69],
# [ 96, 114, 132]],
# [[111, 126, 141],
# [174, 198, 222]],
# [[195, 216, 237],
# [276, 306, 336]]])
행렬곱은 흔히 dot 연산과 matmul 연산으로 가능한데, 2차원 이하에서는 두 함수는 똑같이 동작하지만 3차원에선 차이가 있다고 한다.
다음으로 einsum 연산은 행을 i, 열을 j등으로 표기하여 간단하게 수행할 수 있는 연산이다. 아인슈타인 표기법에 대한 연산이다.
a = tc.arange(25).reshape(5,5)
b = tc.arange(15).reshape(5,3)
c = -tc.arange(15).reshape(5,3)
a, b, c
# (tensor([[ 0, 1, 2, 3, 4],
# [ 5, 6, 7, 8, 9],
# [10, 11, 12, 13, 14],
# [15, 16, 17, 18, 19],
# [20, 21, 22, 23, 24]]),
# tensor([[ 0, 1, 2],
# [ 3, 4, 5],
# [ 6, 7, 8],
# [ 9, 10, 11],
# [12, 13, 14]]),
# tensor([[ 0, -1, -2],
# [ -3, -4, -5],
# [ -6, -7, -8],
# [ -9, -10, -11],
# [-12, -13, -14]]))
다음과 같은 행렬 a, b, c에 대하여
# a의 대각합
tc.einsum('ii', a) # tensor(60)
# a의 대각원소
tc.einsum('ii->i', a) # tensor([ 0, 6, 12, 18, 24])
# b의 전치행렬
tc.einsum('ji', b)
# tensor([[ 0, 3, 6, 9, 12],
# [ 1, 4, 7, 10, 13],
# [ 2, 5, 8, 11, 14]])
# a와 b의 행렬곱 계산 (matmul과 결과가 동일함을 확인할 수 있다)
tc.einsum('ij,jk->ik', a, b), tc.matmul(a,b)
# (tensor([[ 90, 100, 110],
# [240, 275, 310],
# [390, 450, 510],
# [540, 625, 710],
# [690, 800, 910]]),
# tensor([[ 90, 100, 110],
# [240, 275, 310],
# [390, 450, 510],
# [540, 625, 710],
# [690, 800, 910]]))
# 같은 모양의 텐서 b,c의 각 행끼리의 점곱
tc.einsum("ij,ij->i", b, c)
# tensor([ -5, -50, -149, -302, -509])
이렇게 어떨땐 합으로, 어떨땐 곱으로 등 되게 다양하게 계산된다. 따라서 자세한 내용은 따로 공부해야할 듯. 너무 깊이 들어가진 말자.
backward 메서드
역전파를 실행시켜 자동미분 및 그래디언트 계산을 쉽게 해주는 텐서 객체의 메서드이다.
기존에 사람이 계산하던 방식대로라면 야코비안 행렬(Jacobian Matrix)을 일일이 곱해야했겠지만, 여기선 자동으로 역전파를 흘려보내 모든 그래디언트 값을 각 노드에 저장시킬 수 있게 한다.(이 경우 requires_grad=True로 설정해야함)
역전파를 보낸 후 그래디언트 값은 .grad를 통해 확인할 수 있다. 후에 경사하강법(Gradient Descent)을 실행하는 과정에서 가중치를 갱신한 후 해당 그래디언트들을 초기화하여야한다.
grad 파라미터는 사라지지 않고 각각의 노드에서 중첩되어 누적되기 때문으로, 이 경우 올바른 독립적 계산을 할 수 없다. 그래디언트 초기화는 x.grad=None이나 x.detach(), x.grad.zero_(), model.zero_grad() 등의 방식으로도 가능하다.
예시 코드를 보자.
tensor = tc.linspace(-5, 5, 20, requires_grad=True)
F = tensor ** 2 # shape-(20)인 텐서
F_sum = F.sum()
F_sum.backward()
#F.backward()
tensor.grad
# tensor([-10.0000, -8.9474, -7.8947, -6.8421, -5.7895, -4.7368, -3.6842,
# -2.6316, -1.5789, -0.5263, 0.5263, 1.5789, 2.6316, 3.6842,
# 4.7368, 5.7895, 6.8421, 7.8947, 8.9474, 10.0000])
범용적인 경사하강법 코드를 하나 소개할 건데, 전체적인 구성은 다음과 같다.
def descent_down_2d_parabola(w_start, learning_rate, num_steps):
xy_values = [w_start]
for _ in range(num_steps):
xy_old = xy_values[-1]
xy_new = xy_old - learning_rate * (np.array([4., 6.]) * xy_old)
xy_values.append(xy_new)
return np.array(xy_values)
위 코드는 (크기 2짜리) 1차원 벡터에 대한 역전파를 계산하는 과정이다. 이때 w_start는 입력되는 가중치로, 먼저 리스트 형태로 변환해준 후 가장 마지막 원소(xy_values[-1])를 꺼내어 xy_old로 삼는다.
이때 가장 마지막 원소를 꺼내는 이유는, 그것이 현재 존재하는 가중치 중 가장 최신본이기 때문이다. 코드를 보면 알수 있듯이 해당 원소로 새로운 xy_new를 계산한 후 append, 즉 리스트의 맨 뒤에 추가해준다. 다시 for문을 돌아 가장 마지막 원소를 꺼내면 방금 전에 계산된 xy_new가 다시 xy_old가 되면서 계속 갱신되는 과정을 반복하는 것이다.
def gradient_step(tensors, learning_rate):
# isinstance 함수를 이용하여 입력된 tensors가 단일 텐서인지, iterable인지 판단한다
if isinstance(tensors, tc.Tensor):
tensors = [tensors]
# for 문을 이용하여 tensors의 tensor를 하나씩 꺼내며 경사하강을 진행
for t in tensors:
if t.grad is not None:
t.data -= learning_rate * t.grad
t.grad.zero_()
이때 실제 그라디언트 계산을 수행하는 코드를 보면 isinstance라는 파이썬 내장 함수를 통해 iterable(반복가능)한지를 판단하는데, 반복가능하지 않다면 리스트로 바꾸어 반복 가능하게 바꿔준다.
TensorDataset과 Dataloader
이 둘은 torch.utils.data에 저장된 함수들로 DataLoader는 각각의 훈련 데이터와 그 레이블 값을 쌍으로 묶어주는 기능을, DataLoader는 파라미터 batch_size와 shuffle을 통해 배치의 크기 및 셔플 여부를 설정할 수 있다.
예를 들어 이렇게.
from torch.utils.data import DataLoader, TensorDataset
# Prepare the dataset
train_data_tensor = torch.tensor(train_data, dtype=torch.float32)
truth_tensor = torch.tensor(true_f(train_data), dtype=torch.float32)
dataset = TensorDataset(train_data_tensor, truth_tensor)
# 배치 크기와 섞을지 여부만 지정하면 알아서 해줌
dataloader = DataLoader(dataset, batch_size=25, shuffle=True)
# Training loop
learning_rate = 0.01
for epoch_cnt in range(1000):
for batch in dataloader:
batch_tensor, truth_tensor = batch
# 은닉층부터 출력층의 가중치 곱까지의 순전파에서 전달되는 값 구하기
prediction = model(batch_tensor)
# torch의 자동미분 함수를 활용하여 역전파 진행
loss = loss_func(prediction, truth_tensor)
# 기울기 초기화
model.zero_grad()
# torch의 자동미분 함수를 활용하여 역전파 진행
loss.backward()
# grad_descent 함수를 이용하여 경사하강의 한 스텝 진행
gradient_step(model.parameters(), learning_rate)
loss_values.append(loss.detach().clone().numpy())
print(f"Epoch {epoch_cnt + 1}----------------------------")
print(f"loss: {loss:.6f}")
출처: OUTTA 24년 여름 AI 부트캠프
(copyright) 해당 내용의 코드 원본 등은 OUTTA에 1, 2차 저작권이 있습니다.