[Deep Learning 3] 미니배치 학습과 SGD(MNIST 활용)

포스팅에 앞서..

과외하랴 인터벌하랴 바빠서 딥러닝 공부를 쉬엄쉬엄하고 있다. 가뜩이나 이 책은 도서관 대출에 1주 연장까지해서 총 3주 안에 끝마쳐야하는데, 그게 당장 다음주 금요일.. 일주일 남았다.

핑계이고 투정이긴한데, DS를 내가 할 수 있을까..하는 생각이 든다. 언제나 후회막심이지만 이거 빼고는 마땅히 하고 싶은 일도 없어서..

이번 포스팅부터는 수식과 코드가 상당히 많아진다. 아마 ‘예상 읽는 시간’은 10분 이상으로 jekyll에 표출되지 않을까..

그래서 수식을 LaTeX를 통해 작성해보려고 한다. 다만 수식이 너무 많아지면 나중에 포스팅을 읽을 때 뭐가 중요하고, 뭐가 곁다리인지 알기 어려워지니까

메인 내용(주 stream)이 아닌 참고자료 및 이론(서브 stream)에 대한 내용은 (*) 표시를 해서 읽을 수 있도록 하겠다. 일단 없는 것부터 읽고, 시간 남으면 *를 읽는 걸로..

LaTeX 표기법에 관하여선 다양한 글이 있으니 적절히 참고하도록 하자.

또 하나 더. 이 책이 나온지 7년이 넘은 책이다보니, 흔히 쓰이는 python 라이브러리 tensorflow와 keras를 사용하지 않는다. 그러다보니 GPU 가동도 안되고 혼파망..

아무래도 다음 책부터는 라이브러리를 활용하는 내용으로 찾아서 읽어야겠다. 이 책은 1~4편까지 있지만 일단 1편만 읽고, 나머지는 나중에 읽는 걸로..

그냥 순수 python 코드로 돌리다보니 시간을 너무 잡아먹고 속도도 지나치게 느리다. 당장 이번 포스팅도 결과가 엉망으로 나오니.. keras를 공부해보도록 하자

신경망 학습

사람이 특징(feature)을 추출해 (레이블 유무와는 별개로) 학습 방식을 지정해주는 머신러닝(기계학습)은 사람의 개입이 들어간다.

그러나 우리가 지금 하고 있는 것은 ‘종단간 기계학습(end-to-end ML)’이라 불리는 딥러닝이 아닌가?

지난 포스팅에서는 파라미터를 피클(pkl)에 있는 그대로 불러들여왔지만, 사실 우리가 임의로 지정한 파라미터가 최적의 해가 된다고 판단할 순 없을 것이다.

그렇다면 인간 말고, 데이터 그 자체에서 최적의 파라미터를 찾아가게 할 수는 없을까? 이게 이번 ‘신경망 학습’의 기본 아이디어다. 신경망이 스스로 학습해나간다는 개념이다.

손실 함수

그런데 길을 찾아가려면 일단 지도가 있어야한다. 무일푼으로 아무 것도 없이 머나먼 여행길을 떠날 수는 없는 노릇이다.

도장깨기를 하고 다니는 포켓몬마스터 지우도 지도를 보고 다니고, 우리의 모험가 도라도 친구 ‘맵(map)’이 길을 안내하는데, 하물며 딥러닝은 없을까?

인간이 그 지도를 만들기 시작했으니, 이를 손실 함수(loss function)라고 한다. 최소화 문제에선 비용 함수(cost function)라고도 하고, 최대화 문제에선 유틸리티 함수(utility function)라고도 하지만, 뭐 난 [로스 펑션]이라고 읽는 게 편하다.

가장 흔히 쓰이는 손실 함수로는 MSE(평균 제곱 오차; Mean Squared Error)가 있는데, 수식으로는 다음과 같다.

\[E = \frac{1}{2}\sum_{k}^{} (y_{k}-t_{k})^{2}\]

혹은 (후술할) 최적화까지 나타낸다면

\[\underset{\theta}{min} \frac{1}{N}\sum_{i=1}^{N} \left \| t_{i}-y(x_{i}; \theta) \right \|_{2}^{2}\]

목표로 했던 값(tk)과 출력된 값(yk)간의 차이를 제곱하여 평균을 나눈 식이다. 두 번째 식에 노름(norm)의 오른쪽 위 첨자는 제곱(squared)을, 오른쪽 아래 첨자는 L2 규제임을 나타낸다.

코드로도 쉽게 구현이 된다.

import numpy as np

# MSE(Mean Squared Error; 평균 제곱 오차)
def mean_squared_error(y, t):
    return 0.5 * np.sum((y-t)**2)

소프트맥스로 도출된 두 결과 y를 보고 원-핫 인코딩된 레이블 t와 비교해서 무엇이 더 적절한 답인지 확인해보자

t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0] # '2'가 정답인 원-핫 인코딩

# 예1: 소프트맥스에서 '2'일 확률이 가장 높다고 나옴
y = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0 , 0.1, 0.0, 0.0]
print(mean_squared_error(np.array(y), np.array(t))) # 0.0975, 오차가 작다

# 예2: 소프트맥스에서 '7'일 확률이 가장 높다고 나옴
y = [0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.0, 0.0]
print(mean_squared_error(np.array(y), np.array(t))) # 0.5975, 오차가 크다

오차가 더 작은 첫번째 예가 적절함을 알 수 있다.

또 다른 손실 함수로 CEE(교차 엔트로피 오차; Cross Entropy Error)가 있다.

\[E = -\sum_{k}^{} t_{k}log y_k\]

식을 이해해보면 결국 정답일 때의 확률값만을 자연로그를 씌운 것임을 알 수 있다. 레이블 벡터인 t가 원-핫 인코딩이 되어있어 0과 1로만 구성되는데, 정답에 해당하는 값에만 t=1이 곱해진 것이기에 정답일 때의 출력이 전체 값을 정하는 꼴이 되는 것이다. 코드로는 아래와 같다.

# CEE(Cross Entropy Error: 교차 엔트로피 오차)
# 정답 레이블 벡터는 원-핫 인코딩이기 때문에, '추정컨데 정답인 것'의 확률의 자연로그를 취하게 된다.
def cross_entropy_error(y, t):
    delta = 1e-7 # 진수가 0이되지 않게하여 -inf 방지
    return -np.sum(t * np.log(y + delta))

목적에 따른 손실함수의 종류 (*)

MSE와 CEE를 다룬 이유는 이 둘이 각각 회귀와 분류 문제에서의 양대 손실함수이기 때문이다.

회귀에서는 회귀함수(regression function)와 실측치 간의 차이를 계산해야하기 때문에 MSE를 사용한다. MSE는 이상치(outlier)에 민감하다(이상치가 있으면 계산값이 이상하게 나온다)는 특징이 있긴 하다.

MSE가 L2 노름(유클리드 거리)을 사용하는 반면, L1 노름(멘하탄 거리)을 적용한 MAE(평균절대오차; Mean Absolute Error)도 존재한다. L1 노름답게 식은 제곱 없이 절댓값으로만 이뤄진다.

\[MAE(\theta) = \frac{1}{N}\sum_{i=1}^{N} \left \| t_{i}-y(x_{i}; \theta) \right \|_{1}\]

반대로 분류 문제에서는 CEE가 사용되는데, CEE는 먼저 정보량을 표현하는 방식에서 유래했다.

보통 뉴스 기사는 흔치 않은 일일수록 더 크게 보도된다. 사람들은 확률이 낮은 사건을 더 놀랍게 여긴다. 따라서 정보량의 수식은 확률의 역수에 (값이 너무 커지는 것을 막기 위해) 로그를 취해 표현된다.

\[I(x) = log \frac{1}{p(x)}=-log p(x)\]

이제 엔트로피(entropy)가 나오는데 열역학에서 배우듯이 이것은 불확실성(uncertainty)이나 무작위성(randomness)을 나타내는 말이다. 분산, 즉 확률분포가 클 수록 어떤 사건이 일어날지 예측이 어렵기에, 분산이 클수록 엔트로피도 크다.

엔트로피는 ‘확률 변수의 정보량의 기댓값’으로 정의되며 수식은

\[H(p) = E_{x \sim p(x)}[-logp(x)]=-\int_{x}^{}p(x)logp(x)dx\]

그래프를 그려보면 p(x)=0과 p(x)=1일 때 엔트로피는 0이 되고, p(x)=0.5일 때 가장 큰 값을 갖는다.

크로스 엔트로피(cross entropy)는 두 확률분포의 유사하지 않은 정도(dissimilarity)를 나타내는데, 어떤 확률분포 q로 확률분포 p를 추정한다고 할 때, 크로스 엔트로피는 q의 정보량을 p에 대한 기댓값을 취하는 것으로 정의된다.

\[H(p,q) = E_{x \sim p(x)}[-logq(x)]=-\int_{x}^{}p(x)logq(x)dx\]

그런데 이 크로스 엔트로피가 CEE로 어떻게 연결되는지가 책에 안 나와있다?! 이건 나중에 시간 남으면 이쪽 파트를 수정해서 보완할테니 일단 넘어가자

미니배치 학습

이제 앞서 다룬 ‘신경망을 스스로 학습’시켜보는 작업을 해야하는데, MNIST 데이터셋은 훈련 데이터가 60000개이다. 이걸 일일이 다 손실함수를 계산해서 작업을 하려면 시간이 무지막지하게 들 거다.

그래서 지난 장에서 배치 처리를 배웠듯, 학습도 배치(batch)로 처리할 거다. 이걸 미니배치(mini-batch)라 하는데, 훈련 데이터로부터 일부만을 임의로 골라 학습을 수행하는 방식이다.

미니배치의 크기를 10개로 잡아서 MNIST를 미니배치 방식으로 학습시켜보자.

# 미니배치(mini-batch)=10 으로 MNIST 학습시키기

import numpy as np
import sys, os # 구글 드라이브와 연동용
import pickle # 필요한지는 모르겠는데 일단 써놓음(안전빵)
import requests # 피클이 인식이 안돼서 부득이하게 추가
sys.path.append('/content/drive/<여기에 주소 입력>') # 내가 저장한 구글 드라이브 위치
from mnist import load_mnist # 책의 깃헙 링크에서 가져온 mnist.py 임포트

def sigmoid(x): # 활성화 함수 1
    return 1 / (1 + np.exp(-x))

def softmax(a): # 활성화 함수 2
    c = np.max(a)
    exp_a = np.exp(a - c)
    sum_exp_a = np.sum(exp_a)
    y = exp_a / sum_exp_a

    return y


# load_mnist()는 flatten의 디폴트값이 True로 되어있다. 즉 압축/정규화/원-핫 모두 수행
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)

print(x_train.shape) # (60000, 784)
print(t_train.shape) # (60000, 10). one-hot이라 정답 레이블 행렬의 열이 10개이다.

train_size = x_train.shape[0] # 60000개의 학습 데이터 중
batch_size = 10 # 10개만을
batch_mask = np.random.choice(train_size, batch_size) # 임의로 골라서
x_batch = x_train[batch_mask] # 미니배치 학습 데이터와
t_batch = t_train[batch_mask] # 미니배치 레이블 데이터로 사용하겠다


# (배치용) CEE 구현(원-핫 인코딩 시)
# 앞서 만든 함수의 범용 버전
def cross_entropy_error(y, t):
    if y.ndim == 1: # 배치 처리가 아닌, 스칼라값 하나씩 입력한다면
        y = y.reshape(1, y.size)
        t = t.reshape(1, t.size) # 벡터로 변환하여 계산

    batch_size = y.shape[0]
    return -np.sum(t * np.log(y)) / batch_size

# (배치용) CEE 구현(원-핫 인코딩이 아닌 '숫자' 레이블일 시)
"""
def cross_entropy_error(y, t):
    if y.ndim == 1: # 배치 처리가 아닌, 스칼라값 하나씩 입력한다면
        y = y.reshape(1, y.size)
        t = t.reshape(1, t.size) # 벡터로 변환하여 계산

    batch_size = y.shape[0]
    # 0-1이 아니므로, 각 행별로 t번째(정답) 원소만을 인덱싱하여 계산
    return -np.sum(np.log(y[np.arange(batch_size), t])) / batch_size
"""


# y(소프트맥스 값)와 t(정답 레이블)를 얻기 위한 중간과정(3장 내용 변형)
def init_network():
    url = "https://github.com/WegraLee/deep-learning-from-scratch/raw/master/ch03/sample_weight.pkl"
    response = requests.get(url) # 깃헙에서 다운받은 후
    with open("sample_weight.pkl", 'wb') as file: # sample_weight.pkl로 저장 후
        file.write(response.content)
    with open("sample_weight.pkl", 'rb') as f: # 다시 엶
        network = pickle.load(f)
    return network


def predict(network, x):
    W1, W2, W3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']

    a1 = np.dot(x, W1) + b1
    z1 = sigmoid(a1)
    a2 = np.dot(z1, W2) + b2
    z2 = sigmoid(a2)
    a3 = np.dot(z2, W3) + b3
    y = softmax(a3)

    return y

network = init_network()
for i in range(len(x_batch)):
    y = predict(network, x_batch[i])
    """print(cross_entropy_error(y, t_batch))로 해보니
    (1, 100)과 (1, 10)의 내적이라고 Error가 떴음.
    CEE 계산 과정에서 y가 1차원 벡터라 reshape을 하다보니
    (10, 10)인 t_batch가 (1, 100)으로 바뀌어 생긴 일이었다! 해결!
    """
    print(cross_entropy_error(y, t_batch[i]))
    # [0.08, 1.10, 4.98, 1.99, 0.07, 0.02, 0.03, 0.38, 0.03, 0.17]
    # 미니배치이다보니 부정확한 곳도 있다.(3번에서 CEE가 4.98씩이나..) 그래도 값이 전체적으로 작은 걸 보니 정확한 편

미니배치이지만 꽤 정확하다. CEE 값이 전체적으로 다 작다!

최적화

상당히 긴 내용을 썼지만, 이제 오늘 내용의 전환점에 왔다. 즉 이만한 내용을 하나 더 쓸 것이다…(오늘 언제 자지..)

신경망 학습 과정에서 기정(旣定)한 파라미터를 갱신해나가는 과정을 최적화(Optimization)라고 한다. 우리는 가장 완벽한 답은 찾을 수 없다. 그러나 주어진 상황에서 최고의 답에 ‘근접한’(혹은 ‘근사한’) 답을 찾으려 노력하는 것인데, 이게 최적화이다.

앞서 보물을 찾기 위해 지도가 필요하다고 했고, 그 지도가 손실 함수라고 말했다. 이제 방향을 읽기 위한 나침반만 있으면 원하는 보물에 다가갈 수 있을 것이다! 그런데 이 나침반(최적화하는 방법)을 어디서 구하지??

최적화는 (후술하겠지만) 사실 편미분이다. 정확힌 그래디언트의 계산이다. 이게 무슨 말이냐고? 일단 잠시 접어두고 미분하는 방식부터 공부해보자.

도함수의 정의에 따라 수치 미분(numerical differentiation)을 해보면

# 미분 구현: 개선
def numerical_diff(f, x):
    h = 1e-4 # 개선 1: 1만 분의 1정도의 값이면 좋은 결과가 나옴
    return (f(x + h) - f(x - h)) / (2 * h) # 개선 2: 전방 차분을 중심 차분으로 바꿈

이와 같은데, 이때 0으로 근사되는 h는 반올림 오차(rounding error) 등 부동 소수점의 한계로 인해 1e-4 정도로 두면 적당하다. 실제로 미분을 해보면

# 수치 미분 예제: 이차 함수
import numpy as np
import matplotlib.pylab as plt

def function_1(x):
    return 0.01*x**2 + 0.1*x

# x = 5일 때의 미분 계수
print(numerical_diff(function_1, 5)) # 0.199..
# x = 10일 때의 미분 계수
print(numerical_diff(function_1, 10)) # 0.299..

# x = 10일 때의 접선
def tangent_line(f, x):
    d = numerical_diff(f, x)
    y = f(x) - d*x
    return lambda t: d*t + y
    # 변수 t에 대한 함수를 넘김
    # 결과적으로 y2 = d*(t - x) + f(x)

x = np.arange(0.0, 20.0, 0.1)
y = function_1(x)
plt.xlabel("x")
plt.ylabel("f(x)")

tf = tangent_line(function_1, 10)
y2 = tf(x) #

plt.plot(x, y)
plt.plot(x, y2)
plt.show()

이렇게 우리가 아는 접선과 같은 형태가 나온다.

그런데 이걸로는 파라미터를 미분할 수가 없다. 왜? 파라미터는 너무 많거든… 지금 다룬 상미분방정식(ODE: Ordinary Differential Equation)으로는 정확히 미분할 수가 없다. 그러면 어떻게 해야 할까?

편미분과 그래디언트

네, 편미분방정식(PDE: Partial Differential Equation)을 쓰시면 됩니다! 답이 바로 나와서 생각할 겨를도 없을 듯 하다.

각 파라미터별로 손실함수를 편미분하면 각 파라미터별 기울기(편미분계수)를 구할 수가 있게 된다.

예를 들어 2행 3열의 가중치행렬 W로 손실 함수 L을 편미분한다면 경사를 다음과 같이 구하게 되는 것이다.

\[W = \begin{pmatrix} w_{11} &w_{21} &w_{31} \\ w_{12} &w_{22} &w_{32} \end{pmatrix}\] \[\frac{\partial L}{\partial W} = \begin{pmatrix} \frac{\partial L}{\partial w_{11}} &\frac{\partial L}{\partial w_{21}} &\frac{\partial L}{\partial w_{31}} \\ \frac{\partial L}{\partial w_{12}} &\frac{\partial L}{\partial w_{22}} &\frac{\partial L}{\partial w_{32}} \end{pmatrix}\]

너무나 깔끔하다. 다음 포물면의 편미분값을 확인하라(편미분하는 연산을 구현한 것은 아니다)

# 편미분 예제: 포물면 (시각화를 위해 식 4.6 변형)
def function_2(x, y):
    return x**2 + y**2
    # 배열 x를 받는다면 return np.sum(x**2)

import numpy as np
import matplotlib.pyplot as plt

fig = plt.figure()
ax = plt.axes(projection = '3d')

x = np.linspace(start = 5, stop = -5, num = 100) # [-5, 5] x 정의역 점 100개
y = np.linspace(start = 5, stop = -5, num = 100) # [-5, 5] y 정의역 점 100개
X, Y = np.meshgrid(x, y) # 두 배열의 모든 원소 쌍 생성
Z = function_2(X, Y) # Z에 포물면 z축 값 리턴

ax.contour3D(X, Y, Z, levels = 50, cmap='cool')
ax.set_title('Paraboloid')

# x=3, y=4일 때 x에 대한 편미분
def function_tmp1(x):
    return x*x + 4.0**2.0

numerical_diff(function_tmp1, 3.0) # 6.000..

# x=3, y=4일 때 y에 대한 편미분
def function_tmp2(y):
    return 3.0**2.0 + y*y

numerical_diff(function_tmp2, 4.0) # 7.999..

반올림 오차를 고려하면 정말 정확하게 나왔다.

자 이제 앞서 본 편미분 행렬을 가지고 계산을 해볼건데, 이 행렬을 그래디언트(gradient)라 부른다. 정확히는 편미분계수들을 단위벡터로 표현한 것이 그래디언트다.

\[\triangledown f = \begin{pmatrix} \frac{\partial f}{\partial x_{1}} &\frac{\partial f}{\partial x_{2}} &... & \frac{\partial f}{\partial x_{n}} \end{pmatrix} f : \mathbb{R}_{n}\rightarrow \mathbb{R}\]

# 그래디언트(Gradient): 함수의 편미분 값을 단위벡터로 정리한 것
import numpy as np

def numerical_gradient(f, x):
    h = 1e-4 # 0.0001
    grad = np.zeros_like(x) # x와 형상이 같은 배열 생성

    for idx in range(x.size):
        tmp_val = x[idx]

        # f(x + h) 계산
        x[idx] = tmp_val + h
        fxh1 = f(x) # fxh1는 스칼라 값

        # f(x - h) 계산
        x[idx] = tmp_val - h
        fxh2 = f(x) # fxh2도 스칼라 값

        grad[idx] = (fxh1 - fxh2) / (2 * h) # 그래디언트 계산
        # x[idx]를 제외한 나머지 값은 변동이 없으므로 함숫값을 빼는 과정에서 자연적으로 소거됨
        x[idx] = tmp_val # 다음 계산을 위해 원래 값으로 복원

    return grad

print(numerical_gradient(function_2, np.array([3.0, 4.0]))) # [6. 8.]
print(numerical_gradient(function_2, np.array([0.0, 2.0]))) # [0. 4.]
print(numerical_gradient(function_2, np.array([3.0, 0.0]))) # [6. 0.]

화살표로 시각화하는 코드까지 덧붙이면 다음과 같이 등고선 비슷하게 출력된다.

import matplotlib.pylab as plt
from mpl_toolkits.mplot3d import Axes3D # 그래디언트 -> 화살표
def function_2(x):
    if x.ndim == 1:
        return np.sum(x**2)
        # 1차원 배열이나 2차원 행렬이 입력하면 function_2()의 매개변수로 1차원 배열이 들어옴
    else:
        return np.sum(x**2, axis=1)
        # 3차원 이상을 입력하면 계산하여 하나의 축으로 합쳐서 반환


def tangent_line(f, x):
    d = numerical_gradient(f, x)
    print(d)
    y = f(x) - d*x
    return lambda t: d*t + y

if __name__ == '__main__':
    x0 = np.arange(-2, 2.5, 0.25)
    x1 = np.arange(-2, 2.5, 0.25)
    X, Y = np.meshgrid(x0, x1)

    X = X.flatten()
    Y = Y.flatten()

    grad = numerical_gradient(function_2, np.array([X, Y]) )

    plt.figure()
    plt.quiver(X, Y, -grad[0], -grad[1],  angles="xy",color="#666666")#,headwidth=10,scale=40,color="#444444")
    plt.xlim([-2, 2])
    plt.ylim([-2, 2])
    plt.xlabel('x0')
    plt.ylabel('x1')
    plt.grid()
    plt.legend()
    plt.draw()
    plt.show()

이 기울기는 각 지점에서 낮아지는 방향(즉 기울기의 결과에 마이너스를 붙인 벡터)으로 그려진 것이다. 따라서 기울기가 가리키는 방향이 각 장소에서 함수의 출력 값이 최소가 되는 방향인 것이다. (이 경우 원점에서 최소가 된다)

어? 드디어 지도와 나침반이 완성되었다. 드디어 보물을 찾으러 갈 수 있다!

경사 하강법

이제 나침반을 따라 서서히 이동해보자. 이 이동하는 방식이 경사 하강법(Gradient Descent)이다. (우리가 최고의 성능을 좇는다면 경사 상승법(Gradient Ascent)을 쓸 수 있다. 근데 부호를 바꾸면 그게 그거 아니냐고? 맞다, 둘은 사실 같은 개념이다)

그런데 코드를 보기에 앞서 주의해야하는 지점은, 막상 내려갔는데 가장 끝까지 내려간 지점이 사실 손실함수가 최소가 되는 지점이 아닐 수 있다는 것이다! 이게 무슨 말이냐?

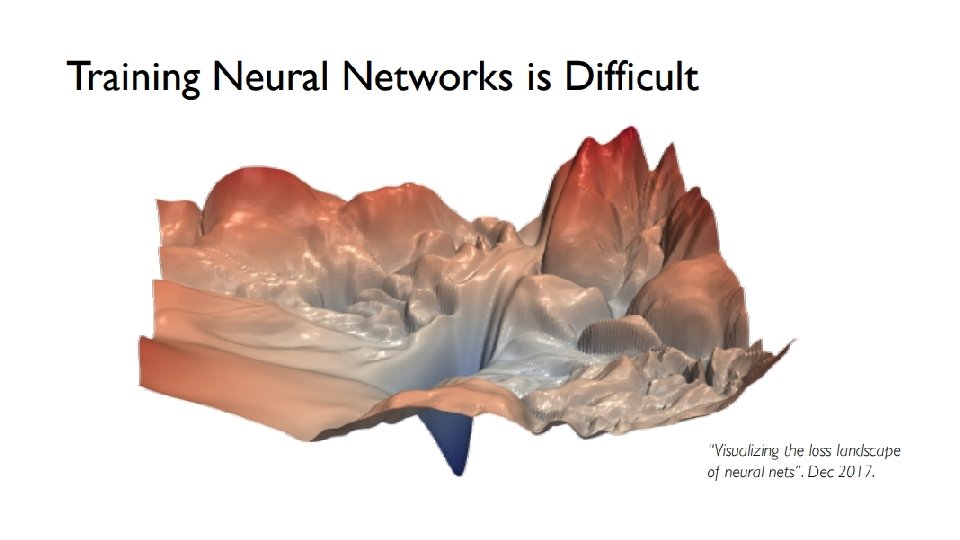
첫째로, 도달한 극솟값 지점이 최솟값이 아닐 수 있다. 손실 함수가 다음과 같이 다차원에서 굴곡이 많다면, 사실 더 낮은 지점이 있음에도, 내가 갖힌 골짜기에선 그곳이 가장 낮은 곳이라 착각할 수 있다는 것이다.

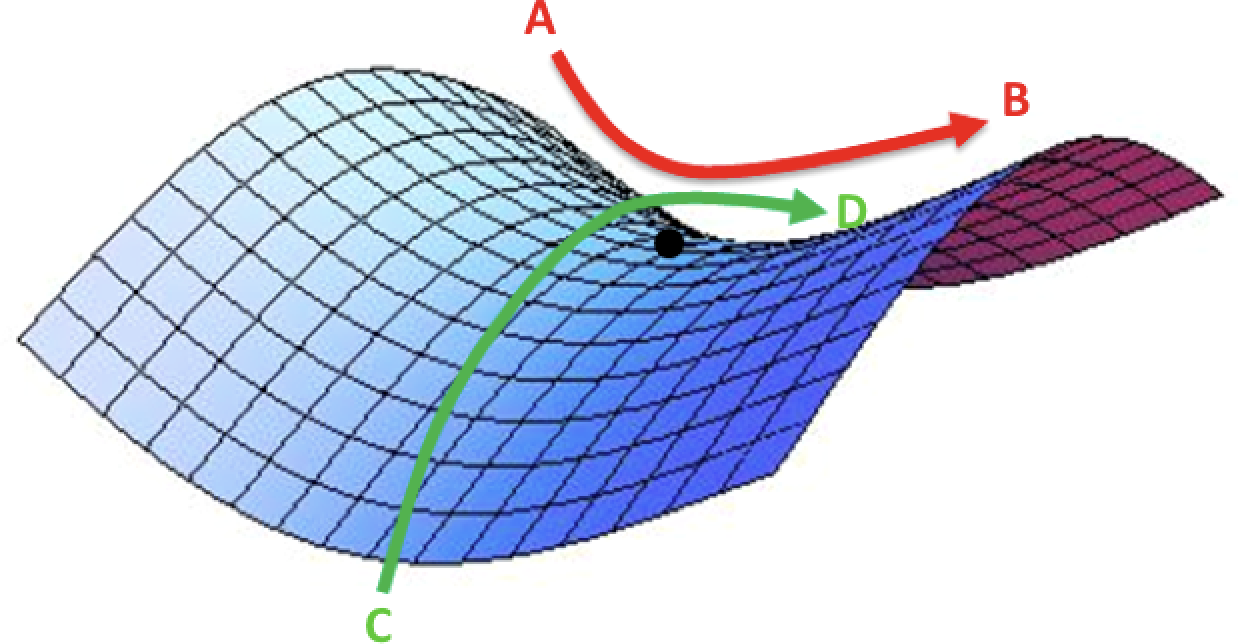
둘째로, 도달한 지점이 사실 안장점(saddle point)일 수 있다. 안장점은 특정 편미분계수는 0이라서 더 내려갈 수 없을 것 같지만, 또 다른 편미분계수는 0이 아니라서 사실 더 내려갈 수 있는 상황을 말한다. 즉 다 내려온 줄 알았는데 사실 착각이었던 것!

주어진 그림에서도 AB방향으로는 최저점이지만, CD방향으로는 아직도 갈 길이 먼 것을 알 수 있다.

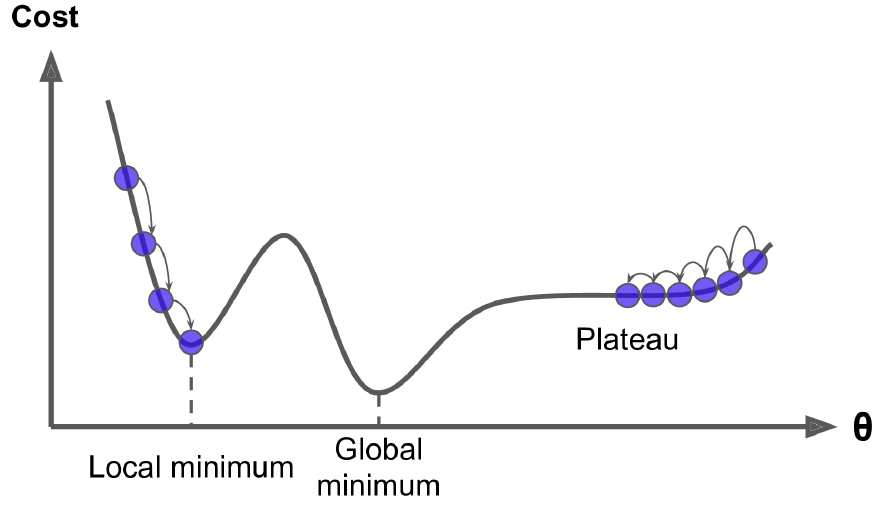
마지막으로, 이동해봤자 고원(plateau)인 경우가 있다. 무슨 말이냐, 최소한 global minimum까진 못가더라도 local minimum은 가야하는데, 고원이라는 평평한 지점에 갖혀 미분계수가 계속 0이 뜨니 더이상 움직이지 못하는 상황을 말한다.

주변을 둘러봐도 다 평지니까 끝인 줄 알았으나, 사실 내려가려면 멀었던 것..

그러면 콜롬버스처럼 인도를 찾아가놓곤 아메리카 원주민들을 인디언이라 우기는 꼴이 되지 않으려면 어떻게 해야할까? 이 문제점들을 해결하기 위한 여러 방법이 있는데, 그중 하나가 학습률(learning rate)을 조정하는 거다. 경사법을 수식으로 나타내면 이해할 수 있다.

\[x_0 = x_0 - \eta \frac{\partial J}{\partial x_0}\]

식을 보면 편미분계수를 왠 n처럼 생긴 계수에 곱하여 기존 파라미터에서 뺌으로써 갱신(경사 하강)을 해간다. 학습률을 나타내는 이 문자는 에타(eta)로 그래디언트를 한 턴당 얼마나 반영할 지를 결정하는 계수이다.

학습률이 너무 작으면 아무리 반복문을 돌려도 minimum에 도달할 수 없고, 너무 크면 minimum을 지나쳐버린다. 즉 학습률은 신경망 학습 과정에서 찾아내는 것이 아닌, 인간이 직접 개입하여 지정해줘야하는 것이다. 이를 하이퍼파라미터라 한다.

# 경사 하강법(Gradient Descent Method) 구현
def gradient_descent(f, init_x, lr=0.01, step_num=100):
    x = init_x

    for i in range(step_num): # step_num번 만큼 반복하여 갱신
        grad = numerical_gradient(f, x)
        x -= lr * grad # 학습률(learning rate)을 grad 행렬에 곱하여 x를 갱신
    return x

# 경사 하강법 예제
def function_2(x):
    return x[0]**2 + x[1]**2

init_x = np.array([-3.0, 4.0])
gradient_descent(function_2, init_x=init_x, lr=0.1, step_num=100) # (0, 0)에 매우 비슷하게 나옴

그럼 이 경사 하강법을 실제로 수행하면 어떻게 되는지 시각화해보겠다.

# 경사 하강법 시각화
# 위의 화살표 그림과 비교해보라. 방향성이 같지 않은가?
import numpy as np
import matplotlib.pylab as plt


def gradient_descent_vis(f, init_x, lr=0.01, step_num=100):
    x = init_x
    x_history = []

    for i in range(step_num):
        x_history.append( x.copy() )

        # 위에서 작성한 numerical_gradient() 함수를 그대로 사용
        grad = numerical_gradient(f, x)
        x -= lr * grad

    return x, np.array(x_history)


def function_2(x):
    return x[0]**2 + x[1]**2

init_x = np.array([-3.0, 4.0])

lr = 0.1
step_num = 20
x, x_history = gradient_descent_vis(function_2, init_x, lr=lr, step_num=step_num)

plt.plot( [-5, 5], [0,0], '--b') # 끊긴 실선으로 x0축
plt.plot( [0,0], [-5, 5], '--b') # 끊긴 실선으로 x1축
plt.plot(x_history[:,0], x_history[:,1], 'o') # 과정을 점으로 찍음

plt.xlim(-3.5, 3.5)
plt.ylim(-4.5, 4.5)
plt.xlabel("X0")
plt.ylabel("X1")
plt.show()

종전에 봤던 화살표 방향대로 최소점을 잘 찾아간다!

그럼 수식에서 벗어나서, 간단한 신경망을 구현해 진짜 경사 하강법을 적용해보자.

# 간단한 신경망을 구현해 경사 하강법 사용
# WegraLee(옮긴이) 깃허브에서 common 폴더를 내 작업 위치로 가져옴
import sys, os
sys.path.append('/content/drive/<여기에 주소 입력>') # 내가 저장한 구글 드라이브 위치
import numpy as np
from common.functions import softmax, cross_entropy_error
from common.gradient import numerical_gradient


class simpleNet:
    def __init__(self):
        self.W = np.random.randn(2,3) # 표준정규분포로 초기화

    def predict(self, x):
        return np.dot(x, self.W)

    def loss(self, x, t):
        z = self.predict(x)
        y = softmax(z)
        loss = cross_entropy_error(y, t)

        return loss


# SimpleNet 클래스로 loss(CEE) 계산
net = simpleNet()
print(net.W) # 가중치 매개변수 확인

# x는 입력 데이터, p는 활성화 함수 적용 전 값, t는 정답 레이블
x = np.array([0.6, 0.9])
p = net.predict(x)
print(np.argmax(p)) # 최댓값의 인덱스. t와 다르더라도, 학습을 통해 같아질 수 있다

t = np.array([0, 0, 1])
print(net.loss(x, t)) # 0.7889


# 더미 w를 매개변수로 하는 함수 f로 그래디언트 계산
f = lambda w: net.loss(x, t)
dW = numerical_gradient(f, net.W)

print(dW)

"""
[[ 0.19590278  0.13150051 -0.32740329]
 [ 0.29385417  0.19725077 -0.49110493]]
"""

오? 진짜 뭔가 나왔다!

수식을 통한 경사 하강법 설명 (*)

내가 참조하고 있는 책에 나온 그림을 토대로 설명한다.

최초의 가중치 w_1_nm은 내적과정과 활성화함수를 거치면서 복잡한 합성함수의 안으로 들어가버린다. 그런데 그래디언트는 이 가중치 w_1_nm으로 손실함수 J를 편미분해야하는 것인데, 이 합성함수를 어떻게 편미분할까?

단순하다. 그냥 체인룰(연쇄 법칙; chain rule)을 이용해 편미분계수들의 연속된 곱의 형태로 계산하면 된다. (단순한가?)

\[\frac{\partial J}{\partial w_{nm}^1}=\frac{\partial J}{\partial y}\cdot \frac{\partial y}{\partial z^2}\cdot \frac{\partial z^2}{\partial a_m^1}\cdot \frac{\partial a_m^1}{\partial z_m^1}\cdot \frac{\partial z_m^1}{\partial w_{nm}^1}\]

자 이걸 계산하면 경사 하강법에 쓰이는 그래디언트의 원소 하나가 완성된다.

\[\frac{\partial J}{\partial w_{nm}^1}=-\frac{1}{N}\sum_{(x,t)\in D}^{N}2(t-y)\cdot 1\cdot w_m^2\cdot ReLU'(z_m^1)\cdot x_n\]

이제 다섯 번 더 반복하면 된다. 와! 너무 쉽다! 참고로 이게 다음 장의 오차역전파법 내용이다.

확률적 경사 하강법(SGD)

그런데 미니배치를 우리가 멋대로 선정하면 아마 테스트데이터에서 좋은 결과를 내지 못할 거다. 그래서 랜덤으로 미니배치를 선정하는 방식을 택하니, 그게 SGD(확률적 경사 하강법; Stochastic Gradient Descent)다.

# SGD 과정에서의 에포크(epoch)당 정확도를 계산하여 시각화하는 과정 추가
# 이번 장의 최종 결과물!!

import sys, os
sys.path.append('/content/drive/<여기에 주소 입력>') # 내가 저장한 구글 드라이브 위치
import numpy as np
import matplotlib.pyplot as plt
from mnist import load_mnist # 이전에 작업 파일로 옮겼던 mnist.py에서 임포트

(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)

# MNIST 데이터셋이므로 (28 * 28인) 784 데이터를 0~9 사이의 숫자로 판독
network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)

train_loss_list = [] # 학습 데이터 손실함숫값 추이
train_acc_list = [] # 학습 데이터 정확도 추이
test_acc_list = [] # 검증 데이터 정확도 추이


# 하이퍼파라미터: 실험자가 직접 설정
iters_num = 100 # 반복 횟수
#(batch_size=100 기준 1회에 1분씩 걸림... 10000회에서 100회로 축소)
train_size = x_train.shape[0]
batch_size = 100 # SGD에서 쓸 미니배치의 크기
learning_rate = 0.1 # 학습률(eta)

# 1에포크당 반복 수
iter_per_epoch = max(train_size / batch_size, 1) # 0 방지


for i in range(iters_num):
    # 미니배치로 쓸 인덱스를 매번 랜덤하게 선정
    batch_mask = np.random.choice(train_size, batch_size)
    x_batch = x_train[batch_mask]
    t_batch = t_train[batch_mask]

    # 기울기(gradient) 계산
    # 다음 장의 오차역전파법을 배우면 더 빠르게 개선 가능
    grad = network.numerical_gradient(x_batch, t_batch)

    # 매개변수 갱신
    for key in ('W1', 'b1', 'W2', 'b2'):
        network.params[key] -= learning_rate * grad[key]

    # 학습 경과 기록
    loss = network.loss(x_batch, t_batch)
    train_loss_list.append(loss)

    # 1에포크당 정확도 계산
    #if i % iter_per_epoch == 0:
    # 그런데 너무 오래 걸려서 그냥 매번 기록으로 바꿈
    if i % 1 == 0:
        train_acc = network.accuracy(x_train, t_train)
        test_acc = network.accuracy(x_test, t_test)
        train_acc_list.append(train_acc)
        test_acc_list.append(test_acc)
        print("train acc, test acc | " + str(train_acc) + ", " + str(test_acc))


# 그래프 그리기
markers = {'train': 'o', 'test': 's'}
x = np.arange(len(train_acc_list))
plt.plot(x, train_acc_list, label='train acc')
plt.plot(x, test_acc_list, label='test acc', linestyle='--')
plt.xlabel("epochs")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
plt.legend(loc='lower right')
plt.show()

자 결과를 보니 완전 망했다~ 학습을 안 시키고 찍어도 0~9 사이니까 10%의 정확도가 나올텐데, 가끔 20% 좀 안되게 나오고 계속 10.2%를 유지한다.

이게 지금 속도가 반복문 1번 돌리는데 1분씩 걸리길래, 기존 10000회(약 16번의 에포크)대로 하면 10000분이 걸리니 반복을 100회로 확 줄인 결과인 걸 감안한다 하더라도 이 정도면 학습을 안 시키니만 못하다. 찍는 게 낫다.

내 코드가 문제일 수도 있겠지만, 가장 큰 원인은 역시 라이브러리를 사용하지 않았기 때문이 아닌가 한다. keras나 tensorflow를 썼으면 이것보다 더 빠르고 정확한 결과가 나왔을 듯. 아무쪼록 정말 열심히 코드를 짜고 또 돌렸다.. 내 노력은 잊지 말아주길..

여담

4장 극초반에 퍼셉트론 수렴 정리(perceptron convergence theorem)에 대한 설명이 있다. 중간에 나오는 미분계수 파트는 loss function을 logistic function으로하고, MSE로 계산한 방식이다. Example 1까진 이해했는데 그정도면 내 수준에선 충분하겠지..

원래 이것도 설명하는 포스팅을 달려고했는데, 그냥 해보면 된다. 지금이 절대 자정이 넘은 시각이라 걍 던지고 싶어서 그런 건 절대 아니다. 아무튼 아니다 ㅎㅎ

예상 읽는 시간이 16분 소요로 뜨네.. 대박..

출처: [밑바닥부터 시작하는 딥러닝 Chapter 4]

참고: [Do it! 딥러닝 교과서 p.90~106, 115~120, 132~144]