[Deep Learning 4] 오차역전파법(MNIST 활용)

오늘은 어제처럼 힘들지 않았다. 3시간 반만에 한 챕터를 끝냈다! 수식적으로도 흥미로웠고, 무엇보다 colab에서 코드가 정말 빨리 돌아가서 좋았다. 괜히 backprop을 쓰는 게 아니야..

계산 그래프와 역전파

이번 파트를 이해하기 위해선 계산 그래프(computational graph)를 이해해야 한다. 자료구조론에서 말하는 그 ‘그래프’가 맞다. 노드(node)와 엣지(edge)로 이루어진 그 그래프.

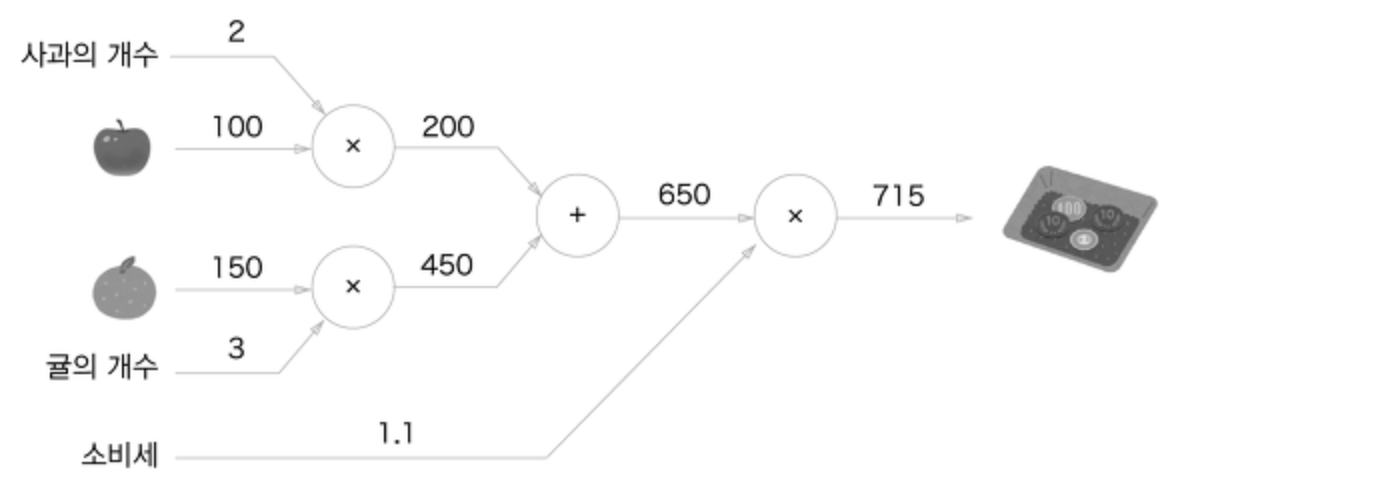
교재의 도식을 빌려보자. 사과 2개와 귤 3개를 사고, 전체 금액의 10%가 소비세로 붙는 형태의 수식을 계산 그래프로 표현한 것이다. 노드에는 연산 기호가 들어가고, 각 엣지에 입력이 전파되어온다. 왼쪽에서 오른쪽으로 이해하는 아주 단순한 단방향 구조이다.

이렇게 계산을 (왼쪽에서 오른쪽으로) 순차적으로 진행하는 것을 순전파(forward propagation)라고 한다. 순전파를 계산 그래프로 표시함으로써 얻는 이익은, 복잡한 계산을 간단하고 국소적인 노드로 이해할 수 있다는 것이다.

또 중간과정에 계산된 값들을 각 노드 클래스의 프로퍼티로 저장하고 있다가 필요할 때 꺼내 쓸 수 있다는 이점도 있다. 그런데 왜 이 이야기를 하느냐?

지난 장에서 딥러닝의 파라미터를 조정하기 위해 그래디언트를 계산하는 법을 배웠다. 그런데 기존의 ‘수치 미분’(도함수의 정의를 활용했던 그 코드)은 너무 느렸고, 원하던 결과도 나오지 않았다(뭐 이건 내 잘못이겠지만)

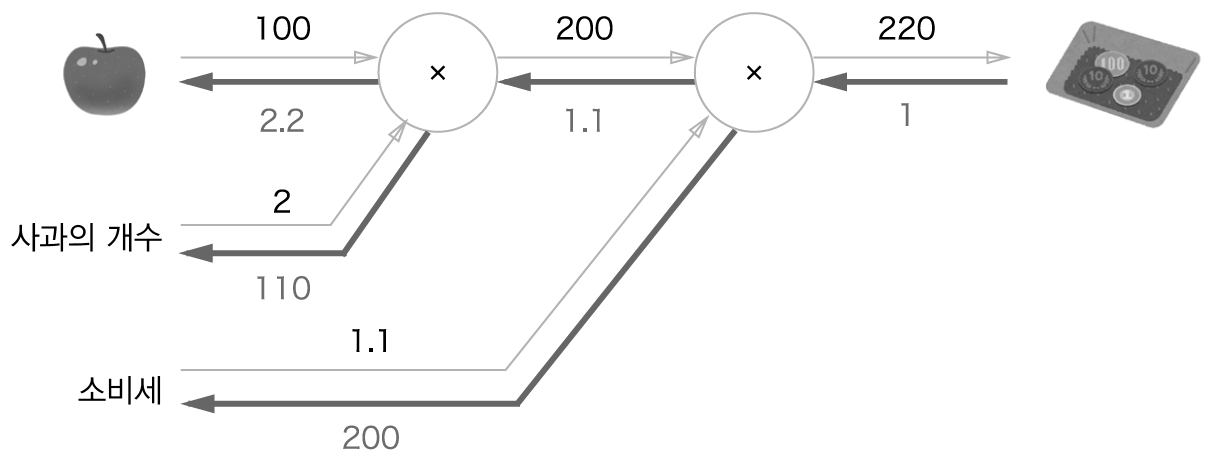
그런데 다음과 같이 거꾸로 오른쪽에서 왼쪽으로 서서히 미분계수들을 곱해가면, 순전파로 계산했을 때와 똑같이 d(총액)/d(사과)가 2.2가 나오는 것을 확인할 수 있다. 즉 체인 룰(연쇄 법칙)을 반대 방향부터 적용해가는 방식이다.

이 방식이 유용한 것은, 일일이 모든 가중치와 편향 원소들로 편미분 식을 계산하는 것보다, 가장 마지막 노드(라는 유일한 상류)에서 최초의 원소들 방향으로 계산해 내려가는 것이 계산의 중복을 덜어주기 때문이다.

이 방식을 역전파(back propagation)라고 하는데, 이는 중간계산결과를 공유함으로써 모든 그래디언트 수치를 한 줄기로 구할 수 있다는 장점이 있다. 더 복잡한 예제를 보며 자세히 살펴보자.

덧셈/곱셈 노드의 역전파

바로 위의 그림을 살펴보면, 곱셈 노드를 기준으로 역전파를 흘려보낼 때, 두 엣지가 갈라지며 서로 상대편의 값을 곱해서 취해감을 확인할 수 있다. 소비세로 총액을 미분한 기울기는 아이러니하게도 사과 2개의 값인 200원을 곱한 수치이다.

반대로 사과 200원으로 총액을 미분한 기울기는 소비세 1.1배의 수치와 같다. 결론만 말하자면, 역전파 과정에서 곱셈 노드는 최초 입력값 중 반대편의 값을 갖고 하류로 내려간다!! 다른 그림도 봐보자.

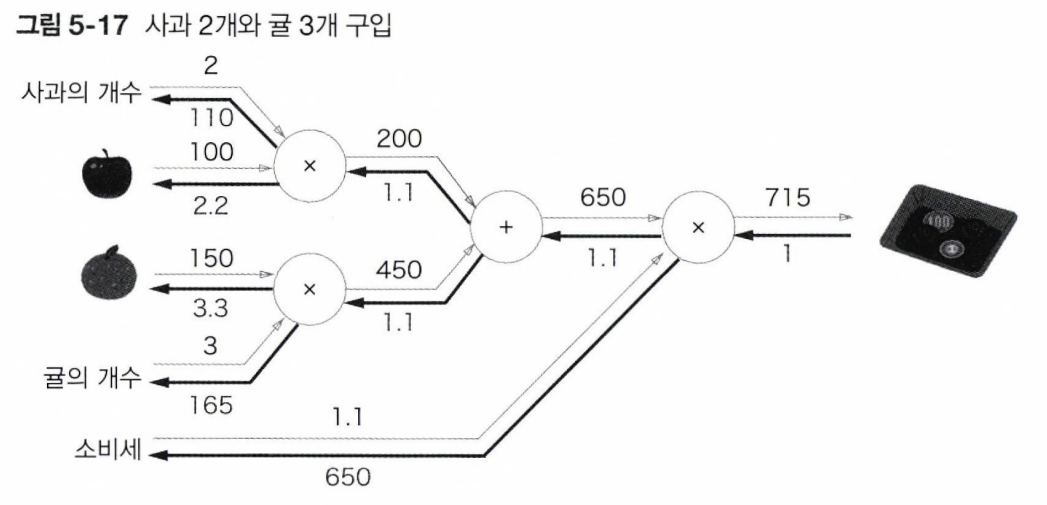
한 개에 100원인 사과 두 알과, 한 개에 150원인 귤 3개를 사고, 소비세 10%가 붙어 715원을 결제하는 상황이다. 여기서 각 노드(변수)별 기울기를 구해보면, 중간의 덧셈 노드 전후로 기울기가 똑같이 1.1인 것이 보이는가?

이는 편미분의 특성 때문인데, 편미분의 경우 x에 대한 미분을 하면 그 이외의 변수(y, z등)는 상수 취급되어 미분돼 0으로 사라지게 된다. 따라서 여러 입력 수치가 순전파를 통해서 갔더라도, 역전파로 되돌아올 경우 상류의 입력된 값을 그대로 하류로 보내게 된다는 것!

코드를 통해 만나보자.

# 곱셈 노드 구현
class MulLayer:
    def __init__(self):
        self.x = None
        self.y = None

    def forward(self, x, y):
        self.x = x
        self.y = y
        out = x * y

        return out

    def backward(self, dout):
        dx = dout * self.y # x와 y를 바꾸어 곱한다
        dy = dout * self.x

        return dx, dy


# 사과 2개 구입의 예: 순전파
apple = 100
apple_num = 2
tax = 1.1

# 계층들
mul_apple_layer = MulLayer()
mul_tax_layer = MulLayer()

# 순전파
apple_price = mul_apple_layer.forward(apple, apple_num)
price = mul_tax_layer.forward(apple_price, tax)

print(price) # 220


# 사과 2개 구입의 예: 역전파
# 호출 순서가 순전파와 반대, '순전파의 출력에 대한 미분'을 인수로 받음
dprice = 1
dapple_price, dtax = mul_tax_layer.backward(dprice)
dapple, dapple_num = mul_apple_layer.backward(dapple_price)

print(dapple, dapple_num, dtax) # 2.2 110 200

여기서 중점적으로 보아야할 부분은 MulLayer 클래스의 backward 메소드이다. MulLayer.backward(dout)을 보면 입력값 dout(상류 노드의 편미분계수값)에 각 노드에 입력됐던 두 값을 서로 바꾸어 곱해주는 것을 확인할 수 있다.

덧셈 노드도 살펴보자.

# 덧셈 노드 구현
class AddLayer:
    def __init__(self):
        # 덧셈 노드는 순전파 입력을 저장할 필요가 없다
        pass

    def forward(self, x, y):
        out = x + y
        return out

    def backward(self, dout):
        dx = dout * 1 # 상류에서 받은 값을 하류로 그대로 흘려보낸다
        dy = dout * 1
        return dx, dy


# 사과 2개와 귤 3개 구입의 예: 순전파
apple = 100
apple_num = 2
orange = 150
orange_num = 3
tax = 1.1

# 계층들
mul_apple_layer = MulLayer()
mul_orange_layer = MulLayer()
add_apple_orange_layer = AddLayer()
mul_tax_layer = MulLayer()

# 순전파
apple_price = mul_apple_layer.forward(apple, apple_num) #(1)
orange_price = mul_orange_layer.forward(orange, orange_num) #(2)
all_price = add_apple_orange_layer.forward(apple_price, orange_price) #(3)
price = mul_tax_layer.forward(all_price, tax) #(4)

print(price) # 715


# 사과 2개 구입의 예: 역전파
# 호출 순서가 순전파와 반대, '순전파의 출력에 대한 미분'을 인수로 받음
dprice = 1
dall_price, dtax = mul_tax_layer.backward(dprice) #(4)
dapple_price, dorange_price = add_apple_orange_layer.backward(dall_price) #(3)
dorange, dorange_num = mul_orange_layer.backward(dorange_price) #(2)
dapple, dapple_num = mul_apple_layer.backward(dapple_price) #(1)

print(dapple, dapple_num, dorange, dorange_num, dtax) # 2.2 110 3.3 165 650

여기서도 역전파 과정을 보자. 기존 순전파에서의 계산 순서 1-2-3-4가 역전파에서는 4-3-2-1로 바뀌었다. 그렇다, 통과 레이어의 순서만 뒤집으면 그래디언트가 바로바로 계산되어 나온다.

이때 MulLayer와 달리 AddLayer 클래스는 메소드는 있어도 프로퍼티는 없는데, 역전파 과정에서 상류에서 흘러들어온 값을 그대로 내려보내주기만 하면 되기 때문이다. 즉 기억할 게 딱히 없다는 것

활성화 함수 계층의 역전파

앞서 노드 단위에서의 역전파를 살펴보았다. 이번에도 노드 단위이지만, 적용되는 계산이 다르다. 활성화 함수의 대표주자인 ReLU와 Sigmoid를 살펴보겠다.

\[y = \left\{\begin{matrix} x (x>0)\\ 0 (x \leq 0) \end{matrix}\right.\]

ReLU의 식은 위와 같기에, 미분하면 다음과 같이 0과 1로만 나뉜다.

\[\frac{\partial y}{\partial x}=\left\{\begin{matrix} 1 (x>0)\\ 0 (x \leq 0) \end{matrix}\right.\]

즉 순전파 때의 입력이 0보다 크면 역전파 때 상류의 값을 그대로 하류로 흘려보내면 된다. 0보다 작거나 같았다면(nonpositive) 하류를 막고 신호를 보내지 않는다. 쉽게 말해 스위치와 같다. 따라서 각 노드는 입력치가 nonpositive했는지만 기억하면 된다!

# Relu 노드 구현
# 파이썬은 '할당에 의한 호출'(call by assignment)
class Relu:
    def __init__(self):
        self.mask = None # nonpositive 여부를 저장

    def forward(self, x):
        self.mask = (x <= 0) # 입력 x를 bool 배열로 만들고
        out = x.copy() # x값은 건들지 않기 위해 복사본을 만든 후
        out[self.mask] = 0 # 복사본에 True(nonpositive)로 마스킹된 값은 0으로 초기화

        return out

    def backward(self, dout):
        dout[self.mask] = 0 # 원본에 True(nonpositive)로 마스킹된 값은 0으로 초기화
        dx = dout # 초기화되지 않은 값은 여과 없이 하류로 보내짐

        return dout

sigmoid는 좀 더 복잡하니 일단 계산 그래프의 역전파 과정을 보며 이해해보자.

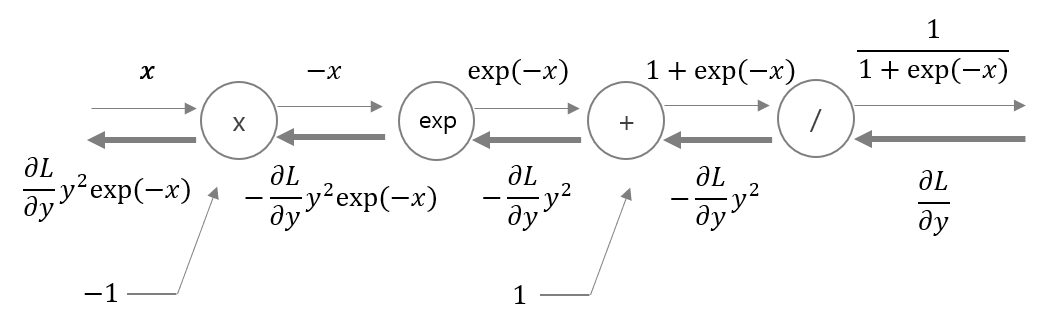
최초 dL/dY라는 값이 하류로 내려올거다. ‘/’ 노드는 역수 계산을 하는 것인데, y=1/x를 미분하면 -1/(x^2)=-y^2이므로 그대로 -y^2이 곱해지는 것을 확인할 수 있다.

그 다음 노드는 덧셈 노드니까 그대로 흘려주고, 자연상수를 밑으로 하는 지수를 취해주는 exp 노드에선 exp(-x)를 미분한 -exp(-x)를 곱해주게 된다. 마지막 곱셈 노드에선 또다른 입력 값이었던 하단의 -1을 곱해 최종적으로 맨 왼쪽의 식이 나오게 된다.

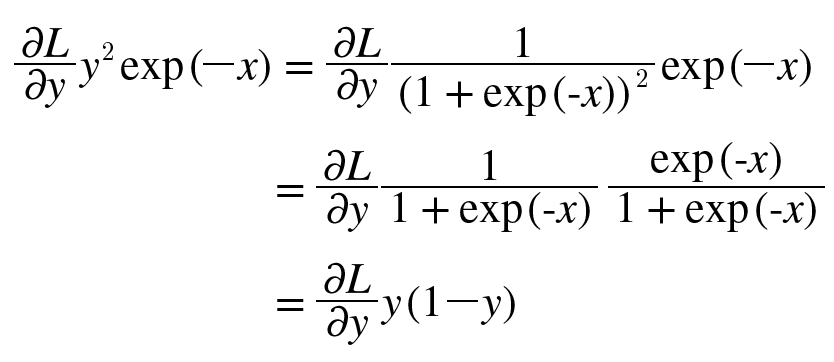
그런데 이 값은 최초의 y가 시그모이드 함수였음을 생각하고 정리해보면 y(1-y)꼴로 변환이 된다!! (실제로 시그모이드 함수를 미분하면 이게 수식적으로 정확함을 확인할 수 있다)

이 변환이 가지는 의미는, sigmoid 계층의 역전파는 순전파의 출력(y)만으로 계산이 된다는 거다. 일일이 도함수 꼴로 계산할 필요 없이, 이렇게 편하게 가능하다니…

# Sigmoid 노드 구현
# (역전파 기준) 상류의 값을 편미분한 것을 기준으로 곱해준다
import numpy as np
class Sigmoid:
    def __init__(self):
        self.out = None

    def forward(self, x):
        out = 1 / (1 + np.exp(-x))
        self.out = out
        return out

    def backward(self, dout):
        dx = dout * (1.0 - self.out) * self.out
        return dx

Affine/Softmax 계층의 역전파

자 이제 본격적으로 계층(은닉층 및 출력층)의 영역으로 들어가보자. 먼저 은닉층에서 활성화함수를 통과하기 전 단계인 Affine 계층이다.

Affine(흔히 [어파인] 혹은 [애핀]이라고 발음) 계층은 최초 퍼셉트론에서 배운 그 식이다.

\[y=x^T\cdot W + b\]

어? 왜 W transpose가 아닌 x transpose냐고? 좋은 질문이다. 파이썬에서 (특히 numpy를 사용하면) 형상의 출력이 (1, 3)과 같은 열벡터가 아닌 (3,)과 같이 행벡터처럼 출력된다. 이걸 적극적으로 적용해 등식의 형상을 억지로 맞추기 위한 하나의 변칙정도로 생각하면 될 듯? (아님 말구~~)

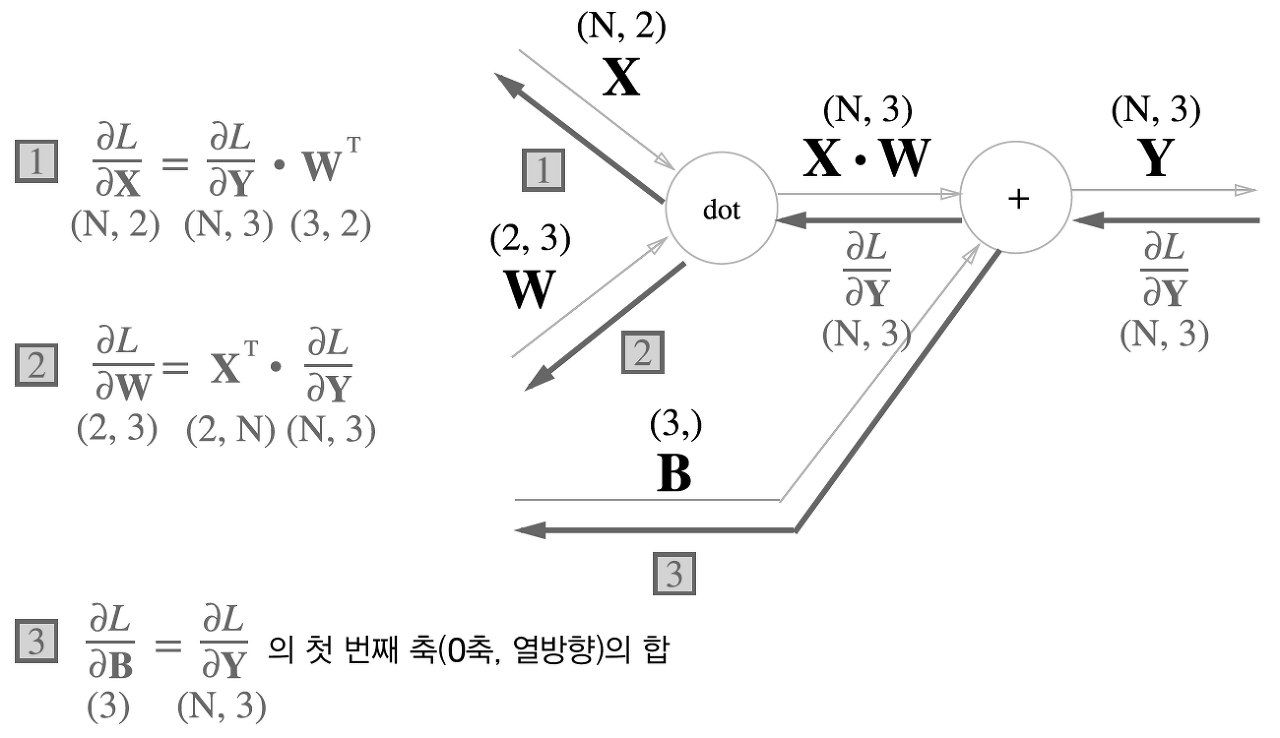
네모 1번과 2번을 보면 전치행렬(transpose)을 편미분계수가 아닌 쪽에 부여함을 볼 수 있다. 형상을 맞추어 행렬곱을 하기위한 작업이다. 여기서 핵심은 각 편미분계수는 뭐에 대하여 미분했는지에 따라 형상이 그대로 따라간다는 것! 이것은 손실함수 L이 하나의 스칼라이기 때문에 강제로 형상이 끌려가는 것이다.

네모 3번을 보면 좌변은 1차원 행벡터, 우변은 2차원 행렬…이라고 생각할 수 있지만? 우변도 1차원 벡터다. 저 dL/dY를 열방향으로 합하여 한 행의 벡터로 축약시킨 것이기 때문이다. 왜 이러냐면, 최초 순전파에서 이미 편향 B 여러 행을 포개서 (n, 3)의 행렬로 입력을 시켰기 때문! 역전파 때는 다시 원래대로 합쳐준다.

여기서 중요한 개념이 하나 나오는데, 입력 과정에서 여러개를 합쳐서 순전파를 보냈다면, 역전파 과정에서는 다시 원래대로 나눠줘야한다는 것이다. 뒤의 softmax 계층에서 다시 한 번 설명하겠다.

# Affine 노드 구현
class Affine:
    def __init__(self, W, b):
        self.W = W
        self.b = b
        self.x = None
        # chatGPT에 물어보니 dW와 db는 추후 갱신(업데이트) 과정에서 사용된다고 함
        # 당장 이 노드에서 사용하는 값은 아니고, 그냥 기록용
        self.dW = None
        self.db = None

    def forward(self, x):
        self.x = x
        out = np.dot(x, self.W) + self.b
        return out

    def backward(self, dout):
        dx = np.dot(dout, self.W.T) # 네모 1번
        self.dW = np.dot(self.x.T, dout) # 네모 2번
        self.db = np.sum(dout, axis=0) # 네모 3번
        """물론 이 처리는 Affine 노드 전의 (상류 노드인) Add 노드에서 했겠지만
        기록을 위해 Affine 노드에도 같은 연산을 해 둔다"""
        return dx

자 이제 오늘 과정에서 가장 어려운 Softmax-with-Loss 계층의 역전파를 다뤄보겠다. 손실함수로는 CEE(교차 엔트로피 오차)를 사용한다. 이름은 거창하지만 소프트맥스(확률 변환)를 통과한 값을 토대로 손실(loss)을 계산해준 것을 통채로 보겠다는 의미다.

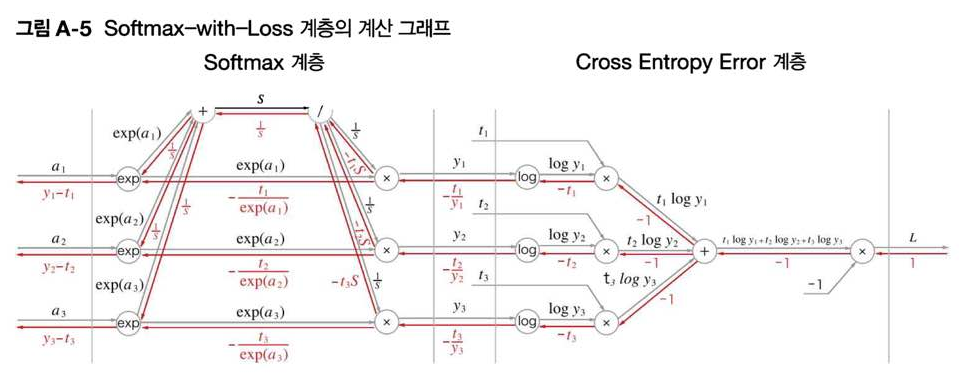
그런데 과정을 보라.. 난 이거 이해했다. (절대 귀찮아서 넘기는 거 아님) 천천히 톺아보며 이해하는데 한 10분? 걸린 것 같다. 하지만 설명하라면 너무 길고, 자세한 계산은 부록(appendix A) 내용이기에 빠른 시일 내에 별도의 포스팅에 적어 두겠다. 이거랑 Identity-with-Loss도!

결론만 보면 (y_i - t_i)다.(도식의 가장 좌측을 보라) 엄청 깔끔하지 않은가? 이게 설계라는데 진짜 무슨 천재가 이걸 고안한건지.. Softmax + CEE의 위엄..

# Softmax-with-Loss 계층 구현
class SoftmaxWithLoss:
    def __init__(self):
        self.loss = None # 손실(순전파 최종결과)
        self.y = None # softmax의 출력(중간결과)
        self.t = None # 정답 레이블(원-핫 벡터)

    def forward(self, x, t):
        self.t = t
        self.y = softmax(x)
        self.loss = cross_entropy_error(self.y, self.t) # 4장에서 구현
        return self.loss

    def backward(self, dout=1): # Loss까지 왔다는 건 최종장이기때문에, 역전파시 입력은 당연히 1이다.
        batch_size = self.t.shape[0]
        dx = (self.y - self.t) / batch_size # batch로 입력했기에 다시 나눠서 각 데이터에 흘러내려줘야함
        return dx

오차역전파법 구현

자 이제 최종 코드로 엮어내보자. 먼저 오차역전파법을 적용하여 신경망을 구현할건데, 4장의 numerical_gradient()가 아닌 새로이 작성하는 gradient() 메소드를 주목하자.

# 오차역전파법을 적용하여 신경망을 구현
# 4장의 수치미분이 아닌 5장의 오차역전파법으로 그래디언트를 계산

import sys, os
sys.path.append('/content/drive/<여기에 주소 입력>') # 내가 저장한 구글 드라이브 위치
import numpy as np
from common.gradient import numerical_gradient
from collections import OrderedDict # 각 계층들의 통과 순서를 지정하기 위해 임포트

class TwoLayerNet:
    def __init__(self, input_size, hidden_size, output_size, weight_init_std=0.01):

        # 가중치 초기화: 행렬 형상에 맞게. 초기화에 대한 자세한 내용은 다른 장에서 후술
        self.params = {}
        self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)
        self.params['b1'] = np.zeros(hidden_size)
        self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size)
        self.params['b2'] = np.zeros(output_size)

        # 계층 생성
        self.layers = OrderedDict() # 순서가 있게 생성. 오차역전파 과정에서 reverse로 뒤집게 됨
        self.layers['Affine1'] = Affine(self.params['W1'], self.params['b1'])
        self.layers['Relu1'] = Relu()
        self.layers['Affine2'] = Affine(self.params['W2'], self.params['b2'])
        self.lastLayer = SoftmaxWithLoss()

    def predict(self, x):
        for layer in self.layers.values():
            x = layer.forward(x) # 순전파: 순서대로 계층을 통과시킴

        return x

    # loss(): 순전파를 작동시킴
    def loss(self, x, t):
        y = self.predict(x)
        return self.lastLayer.forward(y, t) # 마지막에 CEE가 아닌 lastLayer을 순전파로 통과

    def accuracy(self, x, t):
        y = self.predict(x)
        y = np.argmax(y, axis=1)
        if t.ndim != 1 : t = np.argmax(t, axis=1)

        accuracy = np.sum(y == t) / float(x.shape[0])
        return accuracy

    # 이번에는 메인이 아님. 오차역전파법 검증용
    def numerical_gradient(self, x, t):
        loss_W = lambda W: self.loss(x, t)

        grads = {}
        grads['W1'] = numerical_gradient(loss_W, self.params['W1'])
        grads['b1'] = numerical_gradient(loss_W, self.params['b1'])
        grads['W2'] = numerical_gradient(loss_W, self.params['W2'])
        grads['b2'] = numerical_gradient(loss_W, self.params['b2'])

        return grads

    # 오차역전파법 사용
    def gradient(self, x, t):
        # 순전파
        self.loss(x, t)

        # 역전파
        dout = 1
        dout = self.lastLayer.backward(dout) # SoftmaxWithLoss().backward()와 동일

        layers = list(self.layers.values())
        layers.reverse() # 파이썬 list의 reverse 메소드로 layer의 순서를 뒤집음
        for layer in layers: # 뒤집은 계층들을 대상으로
            dout = layer.backward(dout) # 역전파를 통과시킨다

        # 결과 저장
        grads = {}
        grads['W1'] = self.layers['Affine1'].dW
        grads['b1'] = self.layers['Affine1'].db
        grads['W2'] = self.layers['Affine2'].dW
        grads['b2'] = self.layers['Affine2'].db

        return grads

주목할 부분이 2개로, 첫째: 수치 미분은 오차역전파법의 검증용으로만 사용된다는 것. 둘째로 layers.reverse()를 통해 OrderedDict의 리스트의 순서를 반대로 뒤집는다는 것이다. 이는 역전파에서 이용된다.

그러면 기울기 확인(gradient check)을 해보자. gradient 메소드를 numerical_gradient 메소드로 검증하는 방법이다.

# 그래디언트 체크(Gradient Check): 오차역전파법의 결과를 수치 미분으로 검증
import sys, os
sys.path.append('/content/drive/<여기에 주소 입력>') # 내가 저장한 구글 드라이브 위치
import numpy as np
from mnist import load_mnist

(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)

# MNIST 데이터셋이므로 (28 * 28인) 784 데이터를 0~9 사이의 숫자로 판독
network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)

x_batch = x_train[:3]
t_batch = t_train[:3]

grad_numerical = network.numerical_gradient(x_batch, t_batch)
grad_backprop = network.gradient(x_batch, t_batch)

# 각 가중치의 차이의 절댓값을 구한 후, 그 절댓값들의 평균을 낸다
# 0에 가까운 값이 나온다. 즉 오차역전파법으로 구한 그래디언트가 올바르게 계산되었다
for key in grad_numerical.keys():
    diff = np.average(np.abs(grad_backprop[key] - grad_numerical[key]))
    print(key + ":" + str(diff))

3개짜리 배치로 구한 값이긴 하지만, 0에 매우 가까운 값들이 뜨는 것을 보아 오차역전파법 구현이 성공적임을 알 수 있다. 그럼 마지막으로 학습을 진행하고 시각화까지 해보겠다!

# SGD 과정에서의 에포크(epoch)당 정확도를 계산하여 시각화하는 과정 추가
# 4장의 수치미분이 아닌 5장의 오차역전파법으로 그래디언트를 계산
# 5장의 최종 결과물!!

import sys, os
sys.path.append('/content/drive/<여기에 주소 입력>') # 내가 저장한 구글 드라이브 위치
import numpy as np
import matplotlib.pyplot as plt
from collections import OrderedDict # 각 계층들의 통과 순서를 지정하기 위해 임포트
# common 파일과 mnist.py: 옮긴이 깃허브 -> 내 작업 파일로 이동
from common.gradient import numerical_gradient
from common.functions import softmax, cross_entropy_error
from mnist import load_mnist


"""각 노드, 함수 및 계층 구현"""
# Affine 노드 구현
class Affine:
    def __init__(self, W, b):
        self.W = W
        self.b = b
        self.x = None
        # chatGPT에 물어보니 dW와 db는 추후 갱신(업데이트) 과정에서 사용된다고 함
        # 당장 이 노드에서 사용하는 값은 아니고, 그냥 기록용
        self.dW = None
        self.db = None

    def forward(self, x):
        self.x = x
        out = np.dot(x, self.W) + self.b
        return out

    def backward(self, dout):
        dx = np.dot(dout, self.W.T) # 네모 1번
        self.dW = np.dot(self.x.T, dout) # 네모 2번
        self.db = np.sum(dout, axis=0) # 네모 3번
        """물론 이 처리는 Affine 노드 전의 (상류 노드인) Add 노드에서 했겠지만
        기록을 위해 Affine 노드에도 같은 연산을 해 둔다"""

        return dx

# Relu 노드 구현
# 파이썬은 '할당에 의한 호출'(call by assignment)
class Relu:
    def __init__(self):
        self.mask = None # nonpositive 여부를 저장

    def forward(self, x):
        self.mask = (x <= 0) # 입력 x를 bool 배열로 만들고
        out = x.copy() # x값은 건들지 않기 위해 복사본을 만든 후
        out[self.mask] = 0 # 복사본에 True(nonpositive)로 마스킹된 값은 0으로 초기화

        return out

    def backward(self, dout):
        dout[self.mask] = 0 # 원본에 True(nonpositive)로 마스킹된 값은 0으로 초기화
        dx = dout # 초기화되지 않은 값은 여과 없이 하류로 보내짐

        return dout

# Softmax-with-Loss 계층 구현
class SoftmaxWithLoss:
    def __init__(self):
        self.loss = None # 손실(순전파 최종결과)
        self.y = None # softmax의 출력(중간결과)
        self.t = None # 정답 레이블(원-핫 벡터)

    def forward(self, x, t):
        self.t = t
        self.y = softmax(x)
        self.loss = cross_entropy_error(self.y, self.t) # 4장에서 구현
        return self.loss

    def backward(self, dout=1): # Loss까지 왔다는 건 최종장이기때문에, 역전파시 입력은 당연히 1이다.
        batch_size = self.t.shape[0]
        dx = (self.y - self.t) / batch_size # batch로 입력했기에 다시 나눠서 각 데이터에 흘러내려줘야함
        return dx

class TwoLayerNet:
    def __init__(self, input_size, hidden_size, output_size, weight_init_std=0.01):

        # 가중치 초기화: 행렬 형상에 맞게. 초기화에 대한 자세한 내용은 다른 장에서 후술
        self.params = {}
        self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)
        self.params['b1'] = np.zeros(hidden_size)
        self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size)
        self.params['b2'] = np.zeros(output_size)

        # 계층 생성
        self.layers = OrderedDict() # 순서가 있게 생성. 오차역전파 과정에서 reverse로 뒤집게 됨
        self.layers['Affine1'] = Affine(self.params['W1'], self.params['b1'])
        self.layers['Relu1'] = Relu()
        self.layers['Affine2'] = Affine(self.params['W2'], self.params['b2'])
        self.lastLayer = SoftmaxWithLoss()

    def predict(self, x):
        for layer in self.layers.values():
            x = layer.forward(x) # 순전파: 순서대로 계층을 통과시킴

        return x

    # loss(): 순전파를 작동시킴
    def loss(self, x, t):
        y = self.predict(x)
        return self.lastLayer.forward(y, t) # 마지막에 CEE가 아닌 lastLayer을 순전파로 통과

    def accuracy(self, x, t):
        y = self.predict(x)
        y = np.argmax(y, axis=1)
        if t.ndim != 1 : t = np.argmax(t, axis=1)

        accuracy = np.sum(y == t) / float(x.shape[0])
        return accuracy

    # 이번에는 메인이 아님. 오차역전파법 검증용
    def numerical_gradient(self, x, t):
        loss_W = lambda W: self.loss(x, t)

        grads = {}
        grads['W1'] = numerical_gradient(loss_W, self.params['W1'])
        grads['b1'] = numerical_gradient(loss_W, self.params['b1'])
        grads['W2'] = numerical_gradient(loss_W, self.params['W2'])
        grads['b2'] = numerical_gradient(loss_W, self.params['b2'])

        return grads

    # 오차역전파법 사용
    def gradient(self, x, t):
        # 순전파
        self.loss(x, t)

        # 역전파
        dout = 1
        dout = self.lastLayer.backward(dout) # SoftmaxWithLoss().backward()와 동일

        layers = list(self.layers.values())
        layers.reverse() # 파이썬 list의 reverse 메소드로 layer의 순서를 뒤집음
        for layer in layers: # 뒤집은 계층들을 대상으로
            dout = layer.backward(dout) # 역전파를 통과시킨다

        # 결과 저장
        grads = {}
        grads['W1'] = self.layers['Affine1'].dW
        grads['b1'] = self.layers['Affine1'].db
        grads['W2'] = self.layers['Affine2'].dW
        grads['b2'] = self.layers['Affine2'].db

        return grads


"""신경망 학습"""
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)

# MNIST 데이터셋이므로 (28 * 28인) 784 데이터를 0~9 사이의 숫자로 판독
network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)

train_loss_list = [] # 학습 데이터 손실함숫값 추이
train_acc_list = [] # 학습 데이터 정확도 추이
test_acc_list = [] # 검증 데이터 정확도 추이


# 하이퍼파라미터: 실험자가 직접 설정
iters_num = 10000 # 반복 횟수
train_size = x_train.shape[0]
batch_size = 100 # SGD에서 쓸 미니배치의 크기
learning_rate = 0.1 # 학습률(eta)

# 1에포크당 반복 수
iter_per_epoch = max(train_size / batch_size, 1) # 0 방지


for i in range(iters_num):
    # 미니배치로 쓸 인덱스를 매번 랜덤하게 선정
    batch_mask = np.random.choice(train_size, batch_size)
    x_batch = x_train[batch_mask]
    t_batch = t_train[batch_mask]

    # 오차역전파법으로 기울기(gradient) 계산
    grad = network.gradient(x_batch, t_batch)

    # 매개변수 갱신
    for key in ('W1', 'b1', 'W2', 'b2'):
        network.params[key] -= learning_rate * grad[key]

    # 학습 경과 기록
    loss = network.loss(x_batch, t_batch)
    train_loss_list.append(loss)

    # 1에포크당 정확도 계산
    if i % iter_per_epoch == 0:
        train_acc = network.accuracy(x_train, t_train)
        test_acc = network.accuracy(x_test, t_test)
        train_acc_list.append(train_acc)
        test_acc_list.append(test_acc)
        print(str(i) + "th: train acc, test acc | " + str(train_acc) + ", " + str(test_acc))


"""시각화"""
# 그래프 그리기
markers = {'train': 'o', 'test': 's'}
x = np.arange(len(train_acc_list))
plt.plot(x, train_acc_list, label='train acc')
plt.plot(x, test_acc_list, label='test acc', linestyle='--')
plt.xlabel("epochs")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
plt.legend(loc='lower right')
plt.show()

대충 200줄 좀 넘는다. 최초 테스트데이터셋 정확도 12.6%에서 시작해서 10000회 반복만에 96.9%까지 올라왔다. 근데 이미 10번째 에포크에서 96.2% 찍음.. 너무 반복을 많이 할 필요도 없어 보인다.

출처: [밑바닥부터 시작하는 딥러닝 Chapter 5]