1 분 소요

이 글은 Affine/Softmax 계층의 역전파에 대한 포스팅의 후속 포스팅이다. 그중 Softmax-with-Loss 계층의 순전파와 역전파에 대한 설명이다.

Softmax-with-Loss 계층

먼저 해당 계층은 CNN의 가장 말단에 위치한다. 특히 MNIST와 같이 데이터를 분류하는 과정에서 각 클래스에 속할 확률을 softmax 함수로 구하고, 마지막에 손실함수의 loss 값을 구하는 전체 과정을 하나로 압축시킨 계층이다.

Softmax-with-Loss의 순전파

소프트맥스 함수의 수식은 다음과 같다.

\[y_k = \frac{e^{a_{k}}}{\sum_{i=1}^{n}e^{a_{i}}}\]

각 입력 값을 밑이 자연상수인 지수를 취한 후, 지수들의 합으로 나누는 계산이다. 각 지수의 합을 S, 소프트맥수를 통과한 중간 결과를 y_i로 표기하면

\[S = \sum_{i=1}^{n} e^{a_i}\]

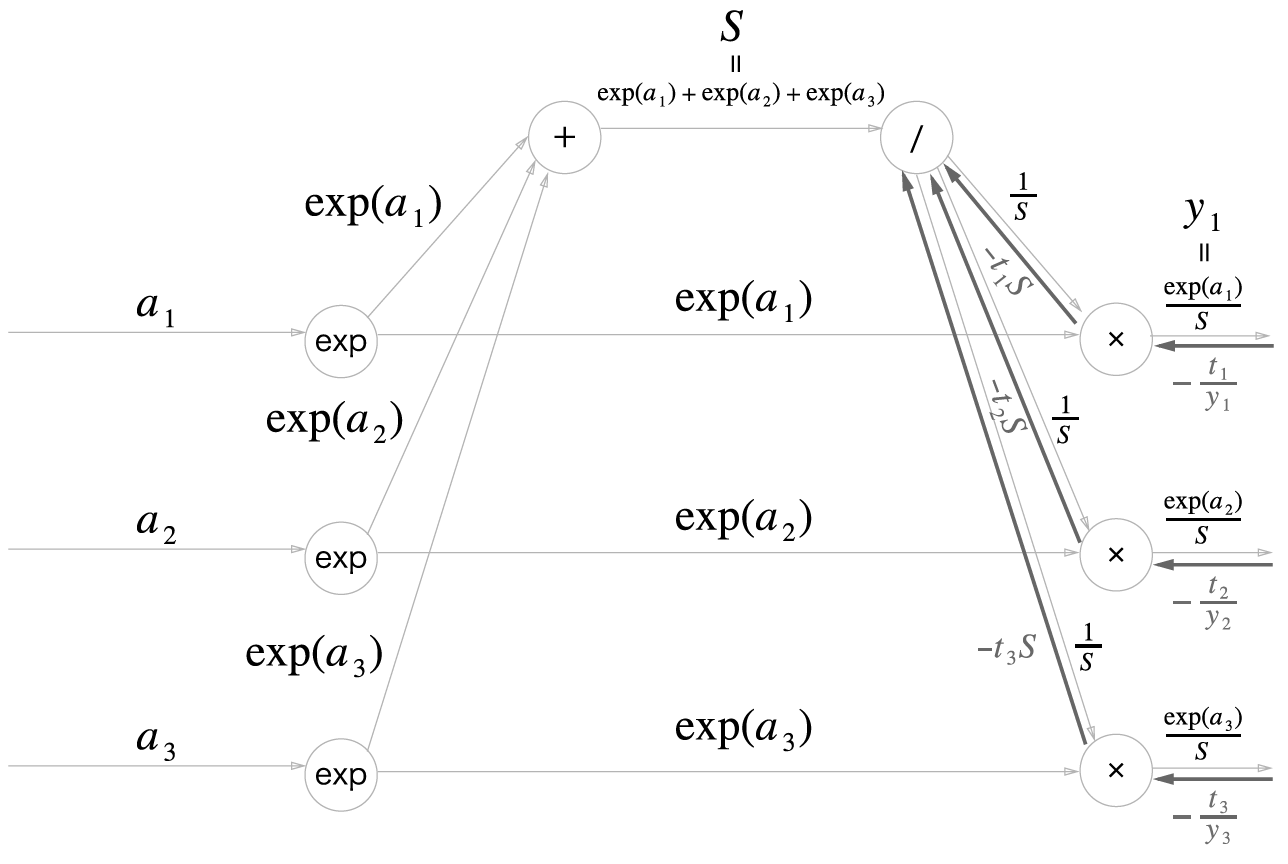
라고 정의하자 위에서 말했으므로

\[y_i = \frac{e^{a_i}}{S}\]

또한 CEE의 수식은

\[L = -\sum_{k}^{}t_k log y_k\]

따라서 손실함수 L을 장황하게 풀어서 쓰자면

\[L = -t_1 log \frac{exp(a_1)}{S} -t_2 log \frac{exp(a_2)}{S} -t_3 log \frac{exp(a_3)}{S}\]

물론 이중 하나의 t를 제외하고는 다 0이기때문에, 식이 길더라도 실제 계산은 매우 간단하게 된다. 뭐 순전파가 이해가 안되는 사람은 없을테고, 핵심은 역전파겠지?

Softmax-with-Loss의 역전파

먼저 역전파의 기본 규칙들을 다시 짚어보자면

  1. 역전파의 초깃값, 즉 최상류(가장 오른쪽의 Loss 노드)에 들어오는 값은 1이다.

  2. 곱셈 노드는 순전파 때의 입력을 서로 바꿔 곱하고 하류로 흘려보낸다.

  3. 덧셈 노드에서는 상류에서 전해진 미분을 그대로 하류로 흘려보낸다.

  4. 로그 노드는 진수의 역수를 곱하여 내려보내준다. 즉

\[y=logx\Rightarrow \frac{\partial y}{\partial x}=\frac{1}{x}\]

여기서 로그의 밑이 자연상수인지는 알 수 없지만, 그래봤자 미분값끼리는 상수배이기 때문에 크게 상관 안 써도 되는 듯 하다!

먼저 Loss 함수쪽(CEE 사용)을 보자면

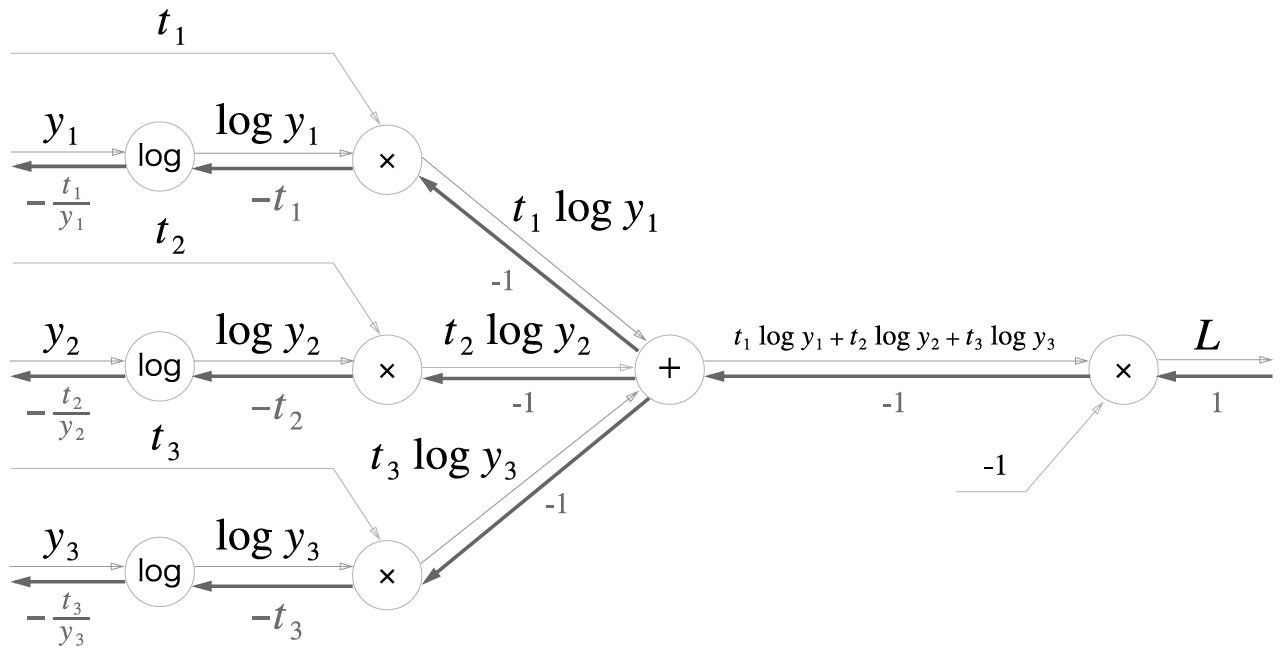
CEE 역전파시 가장 하류 노드에서 나온 값들은 순전파때의 입력(즉 앞서 말한 중간결과)을 y_i라 하면

\[\frac{\partial L}{\partial y}=(-\frac{t_1}{y_1}, -\frac{t_2}{y_2}, -\frac{t_3}{y_3})\]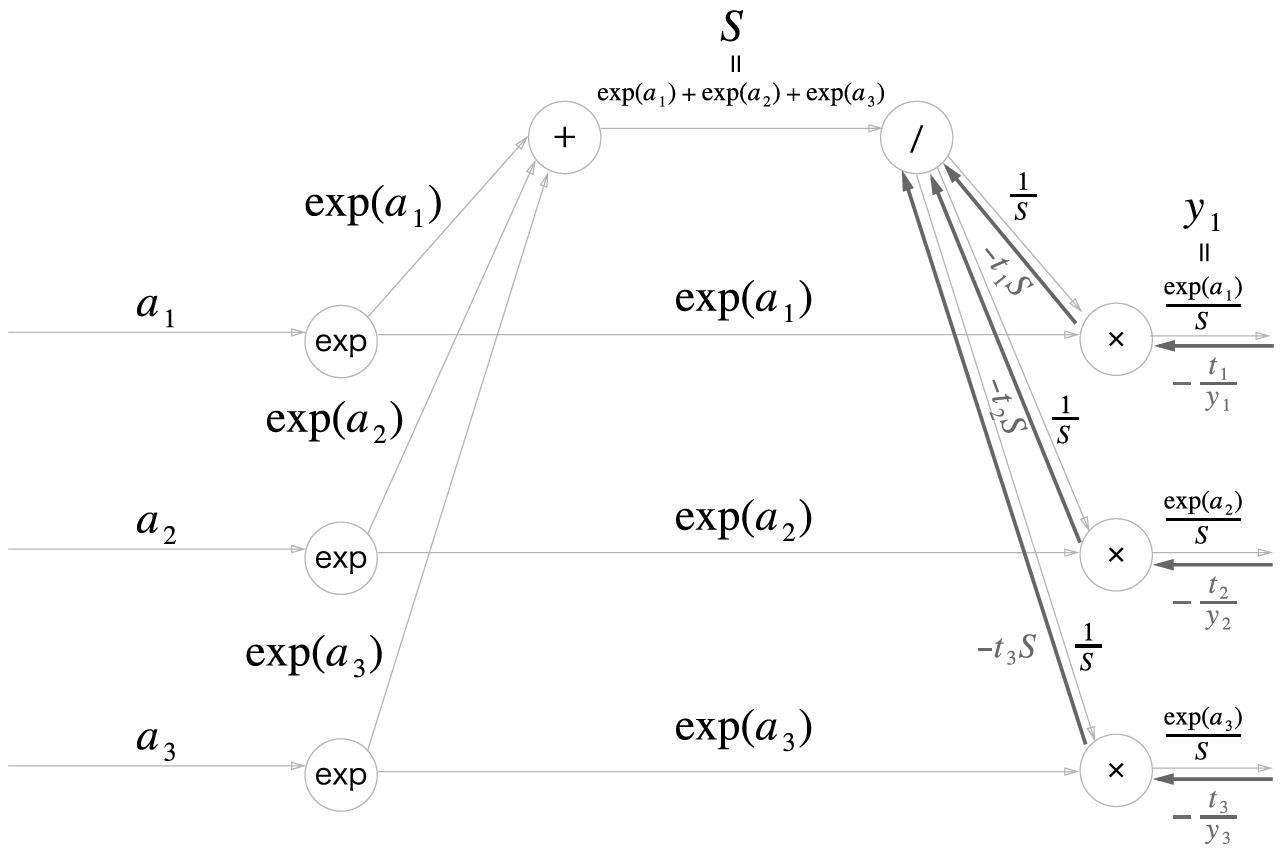

이 값들이 Softmax 계층으로 흘러들어온다. 가장 먼저 맞이하는 곱셈노드에서는 나눗셈 노드쪽으로는 exp(a_i)값들이 곱해진다. 따라서

\[-\frac{t_i}{y_i}\times e^{a_i}=-t_i\times \frac{S}{e^{a_i}} \times e^{a_i}=-t_i S\]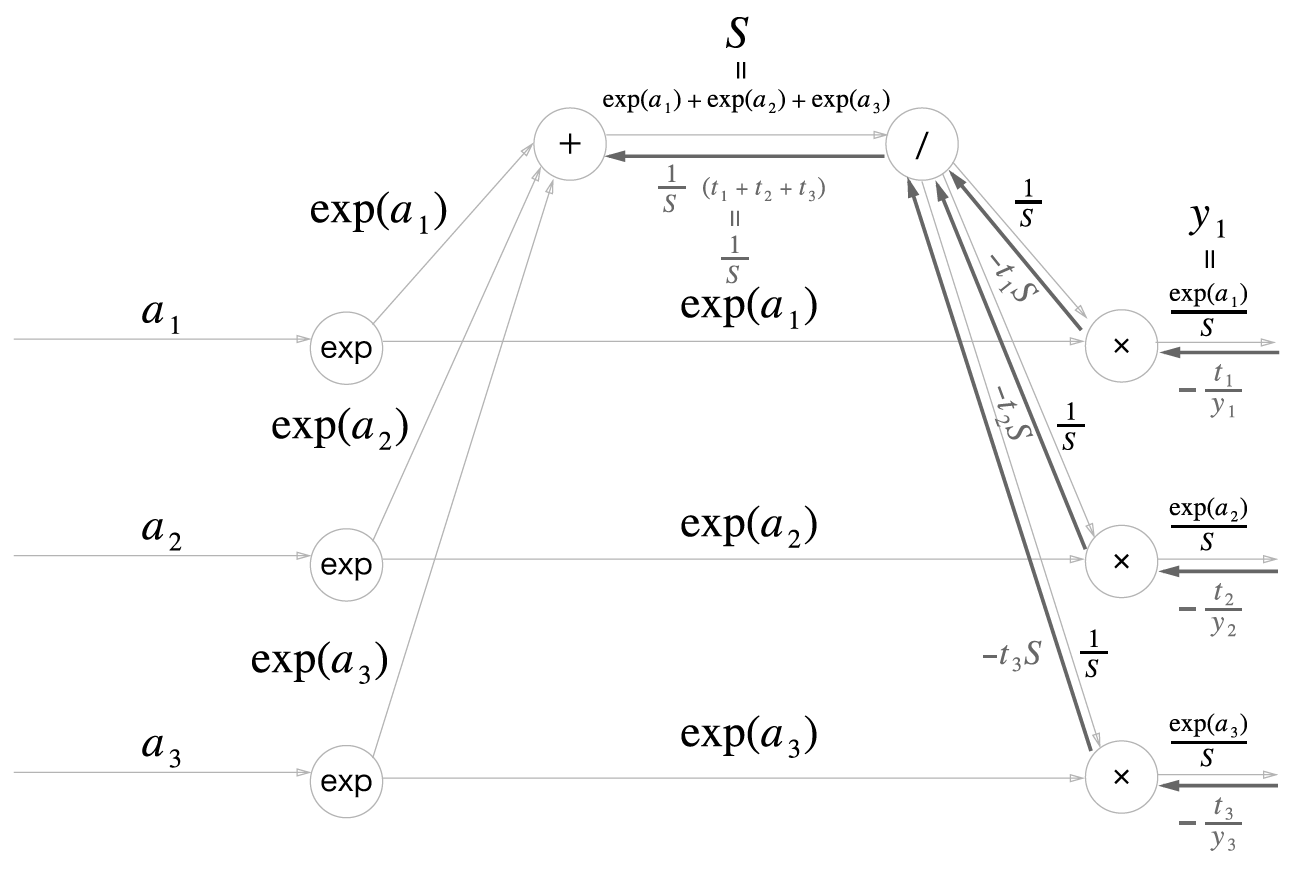

나눗셈 노드에서 순전파의 출력은 1/S였으므로, 역전파시 곱해지는 값은 1/S의 미분값인 -1/(S^2)이다. 따라서

\[-t_i S\times (-\frac{1}{S^2})=\frac{t_i}{S}\]

인데 순전파에서 해당 노드에서 세 곳으로 값이 흘러갔으므로, 역전파시에는 세 곳에서 흘러들어온 값을 합쳐줘야한다. 따라서

\[\frac{t_1+t_2+t_3}{S}\]

인데 순전파 설명 말미에 말했듯 t는 원-핫 벡터 상태라 단 하나의 1을 빼고는 모두 0이다. 따라서 t들의 합은 1일 수밖에 없다. 즉 도식의 덧셈 노드로 흘러들어가는 값은 1/S이다.

\[\frac{t_1+t_2+t_3=1}{S}=\frac{1}{S}\]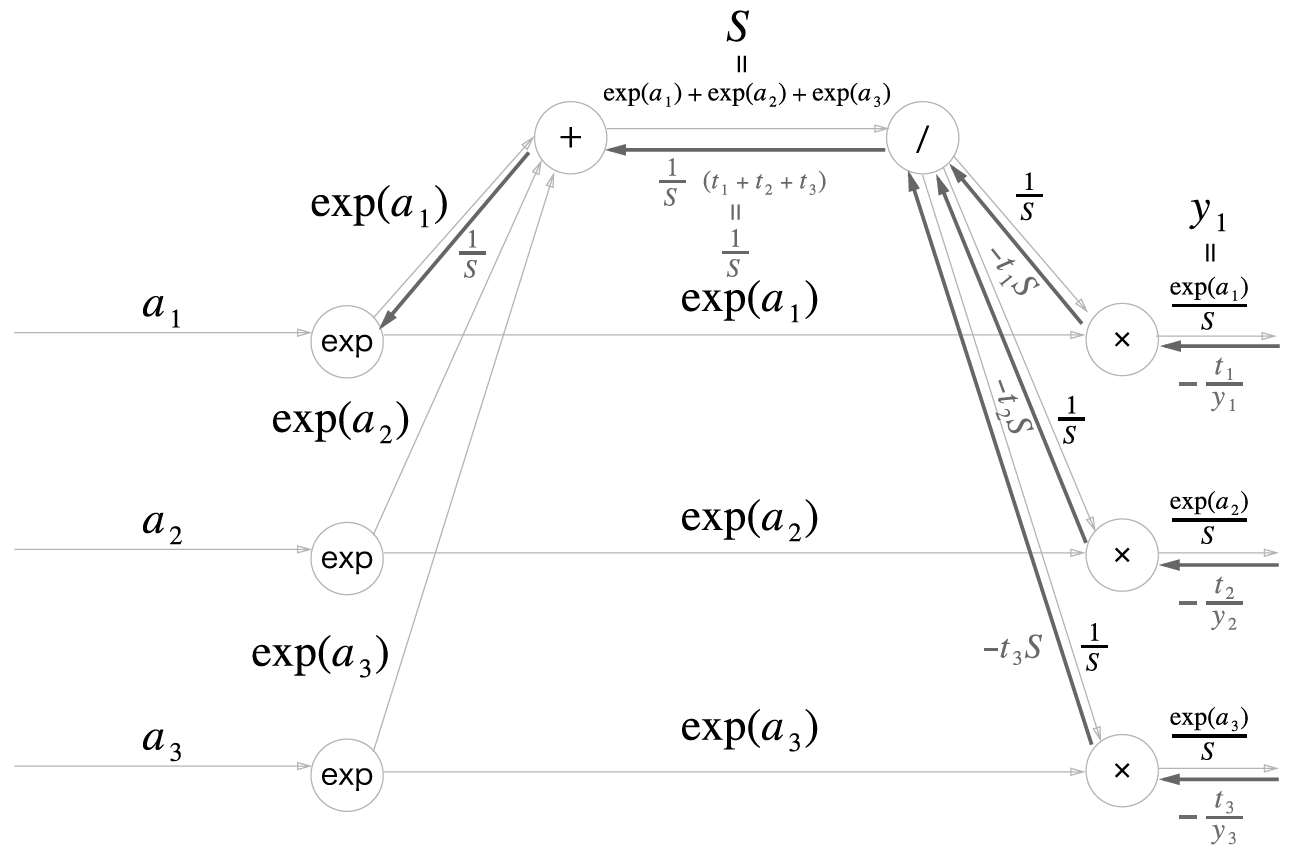

덧셈 노드에선 값을 그대로 흘린다고 하였으므로 역전파 과정에서 들어온 1/S이 그대로 내려간다.

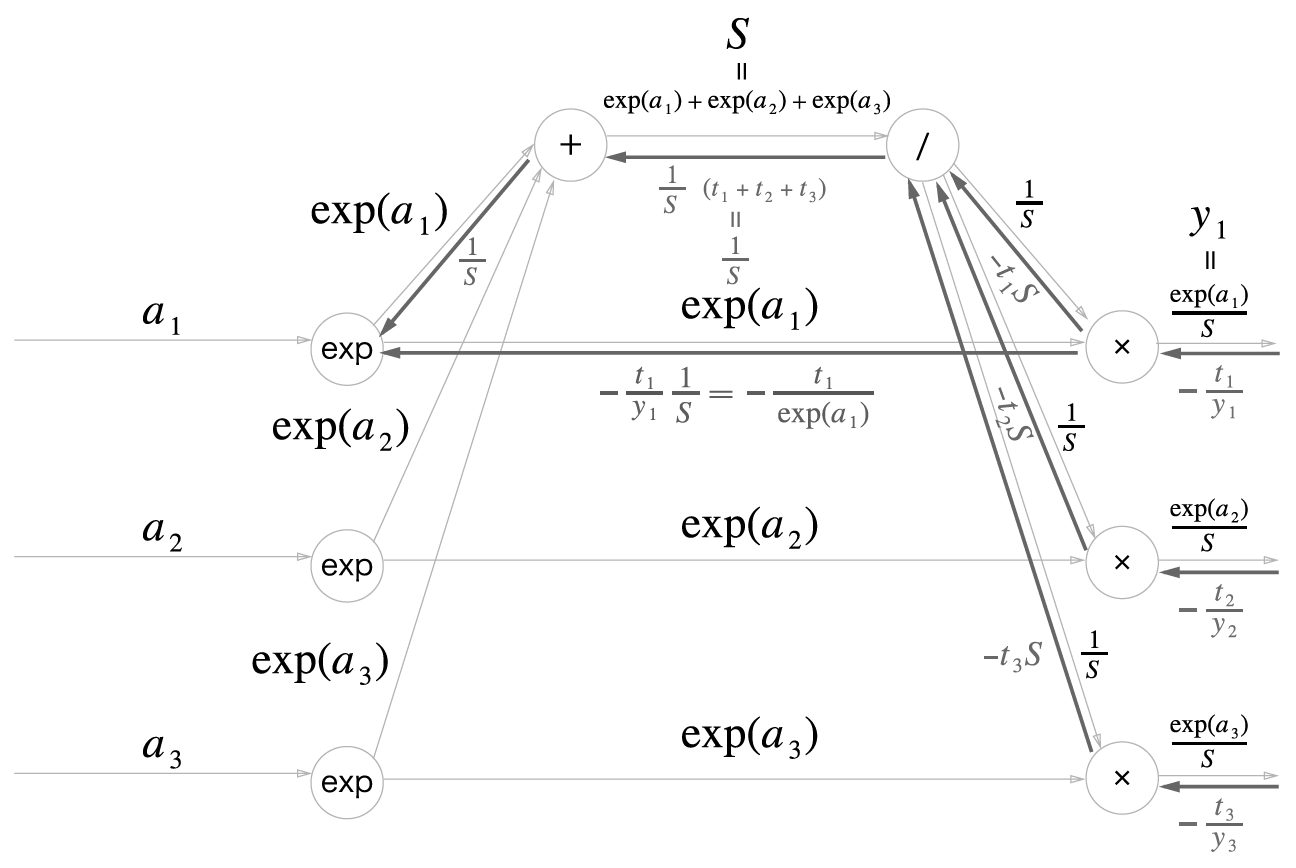
한편 곱셈노드에서 지수노드(exp)로 바로 향하는 흐름의 경우, 1/S이 곱해지므로

\[-\frac{t_i}{y_i}\times\frac{1}{S}=-t_i\times\frac{S}{e^{a_i}}\times\frac{1}{S}=-\frac{t_i}{e^{a_i}}\]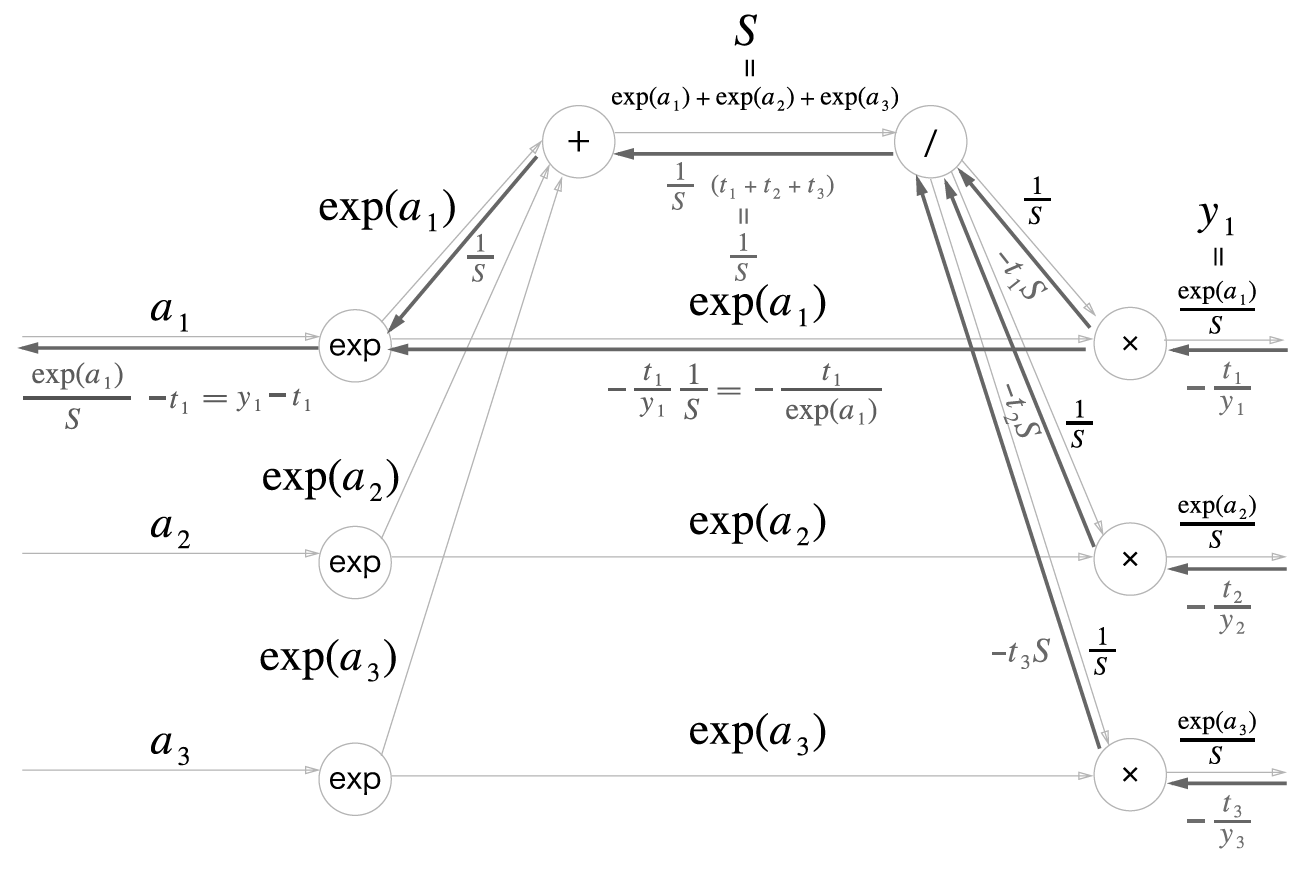

이제 마지막 지수 노드다. 지수함수를 미분하면 자기 자신이므로 그냥 exp(a_i)를 곱해주면 되는데, 두 갈래로 나뉘어서 순전파가 전해졌었으므로 역전파시에는 두 값을 합쳐줘야 한다. 따라서

\[(\frac{1}{S}-\frac{t_i}{e^{a_i}})\times e^{a_i}=\frac{e^{a_i}}{S}-t_i\]

여기서 순전파를 계산할 때 softmax에서 나온 중간 결과 y_i가 e^(a_i)/S라고 앞서 정의했으므로 결국

\[\frac{\partial L}{\partial a}=(y_1-t_1, y_2-t_2, y_3-t_3)\]

즉 Softmax의 결과 y와 CEE의 파라미터 t만으로 Softmax-with-Loss 계층의 역전파를 구할 수 있다! 매우 깔끔하다. 이것을 하나의 도식으로 정리하면 다음과 같다.

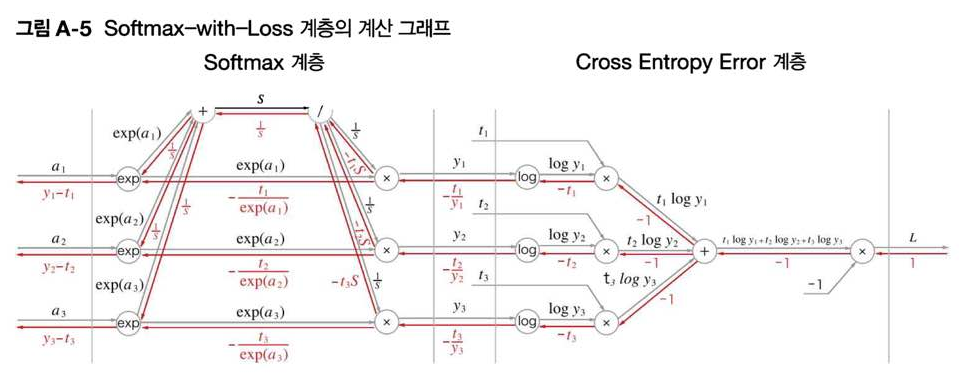
출처: [밑바닥부터 시작하는 딥러닝 Appendix A]

참고