[볼록 최적화 입문 1주차] 볼록 집합
Mar 4 (Tue)
전산수학1을 너무 재밌게 들어서 나중에 ‘백볼록’도 꼭 들어야지라고 생각한지 어연 4년.. 드디어 돌아왔다. 그리운 저 목소리. 그런데 실제로 뵈니 프로필 사진에서 받은 느낌과는 조금 다른 느낌이 들었다. 그래도 백교수님의 ‘추상적 설명’이 내게는 너무나 이해가 잘 되었기에, 이번에도 그 느낌을 받고 싶어 수신을 넣었다.

교재는 스탠포드 Boyd 교수님의 Convex Optimization. 대학원 레벨 중에서도 어려운 교재라고 한다. 인강도 있다고 하니 열심히 과제를 해보자.(영상은 아니고 글) 시험은 과제보다는 살짝 쉬운 정도에서 출제하실 거라고.
한 학기동안 볼록 집합(convex sets)과 볼록 함수(convex functions)를 배우고, 이를 통해 볼록 최적화(convex optimization)을 하는 방법을 배운다고한다. 여기서 최적화란 제약 속에서 목적함수를 최소화(minimize an objective function under certain constraints)하는 것을 말한다.
일반적인 non-convex 문제는 쉽게 풀릴 수도, 쉽게 풀리지 않을 수도 있다. 따라서 복잡도를 단정하기 어렵고 푸는데 오랜 시간이 걸릴 수 있다. 그러나 convex(볼록) 문제는 왠만하면 polynomial한 복잡도로 풀린다고 한다. 우리는 이 과정을 numerically, 즉 컴퓨터의 도움을 받아 한 학기동안 해결해볼 것이다. 따라서 문제를 처음 봤을 때, 이것이 볼록 최적화 문제인지 아닌지를 판단하는 것이 큰 도움이 된다.
전체적인 볼록 최적화 문제의 개형은 다음과 같다.
\[min\;f(x)\quad \text{s.t.}\;x\in A\quad\text{ex. A is }\mathbb{R}^2\]여기서 parameter x는 실수뿐만 아니라 정수, 벡터, 혹은 행렬일 수 있다. 또한 제약은 단순히 집합이 아니라 더 복잡할 수도 있다. non-convex 문제라도 볼록 최적화 문제로 바꾸거나, 근사하거나(approximate), suboptimal한 해를 차용할 수 있다. 따라서 볼록 최적화 문제의 잘 알려진 알고리즘들을 기억해두면 다양하게 적용할 수 있다고.
Mar 6 (Thu)
What is Convex Optimization?
이 과목의 목적은 무엇일까? 볼록 최적화(Convex Optimization)란 ‘볼록 집합에 속한 parameter x가 볼록 함수 f(x)를 구성할 때, 이를 최적화하는 것’을 말한다. 자 최적화가 일반적으로 함수의 최솟값을 구하는 절차라고 배웠다. 그런데 볼록 집합은 무엇이고, 볼록 함수는 무엇인 걸까?
본격적으로 들어가기 전에 표기법(notation) 일부만 정리해두겠다.
\(X\in \mathbb{S}^n\)라는 표기는 행렬 X가 n by n의 대칭행렬(Symmetric matrix)임을 의미한다. (차원이 n차원인 것 같지만, 사실은 n*n임에 주의) 즉 \(\forall x_{i,j}=x_{j,i}\;(i\neq j)\text{ for square matrix X}\) 정방행렬 X는 주대각선을 기준으로 대칭이 된다. 대칭행렬의 경우, 원래 행렬과 그것의 전치행렬이 같다. \(X=X^T\)
기본적으로 벡터는 열벡터로 취급하므로, 같은 차원의 두 벡터 \(x,c\in\mathbb{R}^n\)에 대하여 \(c^Tx\in\mathbb{R}\)는 내적(inner product)로 계산되어 스칼라가 되지만, \(cx^T\in\mathbb{R}^{n\times n}\)는 외적(outer product)로 계산되어 rank-1 matrix가 된다. 이때 rank-1은 행렬 내에서 선형독립인 벡터가 단 1개만 존재한다는 뜻이다. 바꿔말하면 모든 행이 서로 선형 종속이고, 모든 열끼리도 서로 선형 종속이라는 것.
한편 정방행렬 A, B에 대하여 \(AB=BA=I\)가 성립하면 둘을 가역 행렬(Invertible matrix)라 하는데, 어떤 행렬끼리의 곱에 전치(transpose) 혹은 inverse를 적용하면 곱해진 순서가 바뀌게 된다. 또한 전치행렬의 역행렬과 역행렬의 전치행렬은 서로 동일한데, 증명은 다음과 같다.
역행렬의 정의에 따라 \(AA^{-1}=I\) 항등행렬이 된다. 양변에 전치를 취하면 \((AA^{-1})^T=(A^{-1})^TA^T==I^T=I\)이다. 즉 \((A^{-1})^TA^T=I\)라는 관계식에서 역행렬의 정의에 따라 \((A^{-1})^T\)와 \(A^T\)는 역행렬 관계이므로 \((A^{-1})^T=(A^T)^{-1}\)이다.
대칭행렬 Q와 벡터 x \(Q\in\mathbb{S}^n,x\in\mathbb{R}^n\)에 대하여 \(x^TQx\)를 이차 형식(quadratic form)이라 부른다. 이 경우 결국 스칼라값이 되는데, Q가 대칭행렬이 아니라해도 그 중 대칭행렬 성분만이 소거되지 않고 남아 여전히 이차 형식이 된다.
Affine Sets
먼저 선형대수학에서 직선을 정의하는 방법을 살펴야한다. 두 점을 가리키는 임의의 벡터 x1과 x2가 있을 때 선형 결합(weighted sum)
\[\{\theta x_1+(1-\theta)x_2|\theta\in\mathbb{R}\}\]을 직선(lines)이라 부른다. 이때 세타는 실수임에 주목하자. 식을 보면 알 수 있듯 세타가 0이면 점 x2가, 세타가 1이면 점 x1이, 0과 1 사이이면 두 점 사이의 한 지점이, 그 이외에서는 두 점 밖의 한 지점이 됨을 확인할 수 있다. 우리가 아는 직선을 정의하는 방식과 동일하다!

이때 어떤 집합 A에서 임의의 두 벡터 \(x_1,x_2\in \mathcal{A}\)를 통한 선형결합 \(\theta x_1+(1-\theta)x_2\in\mathcal{A}\)이 모든 실수 \(\theta\in\mathbb{R}\)에 대하여 집합 A에 항상 속하면 이 집합 A를 아핀 집합(Affine Sets)이라 한다.
조금 더 이해하기 쉽게 풀어 설명하자면 아핀 집합에서 임의의 두 점을 뽑아 직선을 만들면, 그 직선 상의 점은 해당 아핀 집합에 항상 포함된다.
예를 들어 모든 선형방정식의 해집합은 아핀 집합이다. 선형방정식의 해집합(solution set)
\[S=\{x|Ax=b\}\]을 S라 하면, S는 공집합이거나 해가 하나이거나 해가 무수히 많다. 증명해보자.
임의의 두 해 \(x1, x2\in S\)에 대해 \(Ax_1=Ax_2=b\)가 성립한다. 따라서 앞선 선형결합에 집합 A를 곱한다면 \(A\{\theta x_1+(1-\theta)x_2\}=\theta Ax_1+(1-\theta)Ax_2=\theta b+(1-\theta)b=b\)로 해집합 S의 선형방정식은 참이 된다. 즉 모든 실수 세타에 대하여 직선이 항상 해집합 S 내에 존재하므로, 해집합 S는 아핀 집합이다!
또한 ‘평면 상의 직선(line)’이나 ‘평면 그 자체(whole plane)’는 아핀 집합이다. 다만 반평면(half-plane)은 아핀 집합이 아니다.
Convex Sets
이번에는 선형대수학에서 선분을 정의하는 방법을 살펴보자. 두 점을 가리키는 임의의 벡터 x1과 x2가 있을 때 선형 결합(weighted sum)
\[\{\theta x_1+(1-\theta)x_2|\theta\in[0,1]\}\]을 선분(line segment)이라 부른다. 이때 세타는 닫힌구간 0~1 사이의 실수이다. 세타가 0이면 점 x2, 세타가 1이면 점 x1, 0과 1 사이이면 두 점 사이의 한 지점이 된다.

이때 어떤 집합 C에서 임의의 두 벡터 \(x_1,x_2\in \mathcal{C}\)를 통한 선형결합 \(\theta x_1+(1-\theta)x_2\in\mathcal{C}\)이 0과 1 사이의 \(\theta\in[0,1]\)에 대하여 집합 C에 항상 속하면 이 집합 C를 볼록 집합(Convex Sets)이라 한다.
위의 방식처럼 말로 설명하자면 볼록 집합에서 임의의 두 점을 뽑아 선분을 만들면, 그 선분 상의 점은 해당 볼록 집합에 항상 포함된다. 비교가 되는가? 직선이 아니라 선분이기에 볼록 집합은 아핀 집합에 비해 더 재밌는 모양으로 비교가 가능하다.
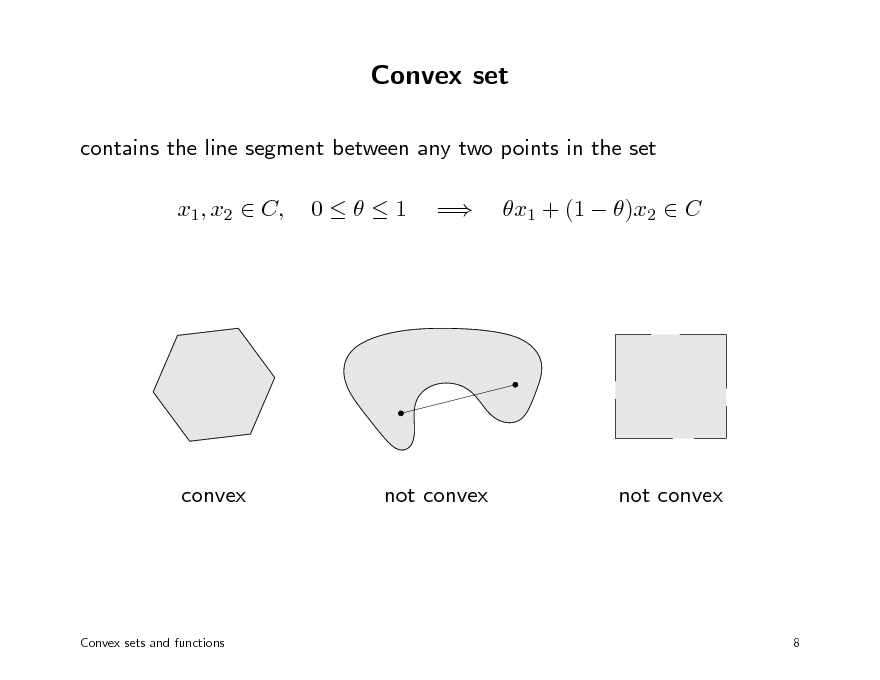
이전과 달리 평면 상의 직선(line)이나 평면 그 자체(whole plane)뿐만 아니라 반평면(half-plane)도 볼록 집합이다. 다만 일부 개구간(열린구간)이 있는 도형이나 도넛 모양, 휜 모양 등은 볼록 집합이 아니다.
일반적으로 이산집합은 볼록 집합이 아니다. discrete한 원소 사이에 낀 실수들이 해당 이산집합에 모두 존재하지는 않을 것이기 때문이다. 다만 원소가 하나인 한원소 집합(singleton set)은 볼록 집합이다. 또한 유한집합은 볼록 집합이 아니지만, 폐구간/개구간/반폐구간의 무한집합은 볼록 집합이다.
출처: 볼록최적화입문(COSE423) ㅂㅅㅈ 교수님