[운영체제 5] 교착 상태(Deadlock)

2024-04-09 7 분 소요

교착(Deadlock)

앞선 [운영체제 4] 포스팅에서 식사하는 철학자 문제를 다루며 ‘교착’에 대해 언급했었다. 이번엔 이 dining philosophers problem과 deadlock에 대해 자세히 짚는 시간을 갖겠다.

모든 프로세스는 실행하기 위해 자원이 필요한데, 이 중 둘 이상의 프로세스가 동시에 임계 구역(critical section)의 코드를 건드리는 것을 레이스 컨디션(race condition)이라 한다고 앞선 포스팅에서 다뤘었다.

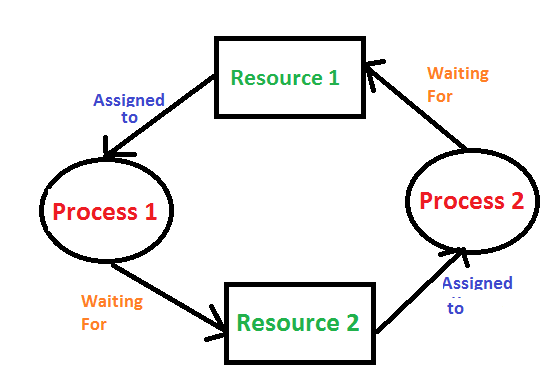
이와는 달리, 둘 이상의 프로세스가 각자 가지고 있는 자원을 무작정 기다리는 것을 교착(deadlock)이라고 한다. 일어나지 않은 사건을 기다리며 진행이 멈춰 버리는 현상인 것.

자원 할당 그래프(Resource-Allocation Graph)

다음의 교착 상태를 살펴보자. 위처럼 어떤 프로세스가 어떤 자원을 사용하고, 또 기다리고 있는지를 표현하는 그래프를 ‘자원 할당 그래프(resource-allocation graph)’라 한다.

자원 할당 그래프에서 프로세스는 원으로, 자원은 사각형으로, 사용 가능한 자원의 개수는 점으로 표현한다. 이중 어떤 프로세스가 자원을 할당받아 사용중이면 자원에서 프로세스를 향해, 기다리고 있다면 프로세스에서 자원으로 화살표를 표시한다.

위의 상황에선 프로세스 P1이 자원 R1을, P2가 P3가 각각 R2의 일부를 사용하고 있으며, P1은 R2를 기다리고 P2는 R1을 기다리고 있는 상황이다.

눈치챘겠지만, 이렇게 원형(환형)의 그래프가 나올 경우 교착 상태가 발생한다고 판단할 수 있다.

코프만 조건(Coffman Conditions)

누군가는 이 원형 그래프를 보고 논문을 쓰고 싶지 않았을까? (그랬다 하자 ㅎ)

그렇다, 에드워드 코프만 주니어 교수(Edward G. Coffman Jr.)가 이에 대해 4가지의 교착 상태 발생 조건을 정립했는데, 이를 코프만 조건(coffman conditions)이라 한다.

각각 상호 배제, 점유와 대기, 비선점, 원형 대기이다. 이 4가지 조건이 모두 만족해야만 교착 상태가 발생할 ‘가능성’이 생긴다. (즉 4가지 모두 만족해도 교착이 아닐 수 있다)

Coffman Conditions

상호 배제(mutual exclusion): 한 프로세스가 사용하는 자원을 다른 프로세스는 사용할 수 없다.
점유와 대기(hold and wait): 프로세스가 자원을 할당받은 상태에서 다른 자원을 할당받기를 기다린다.
비선점(nonpreemptive): 어떤 프로세스도 다른 프로세스의 자원을 강제로 빼앗지 못한다.
원형 대기(circular wait): 자원 할당 그래프가 원의 형태로 그려진다.

교착 상태 해결(Solutions for Deadlock)

그렇다면 어떻게 교착 상태가 일어나지 않도록 하거나 코프만 조건이 충족되지 않도록 할까? 크게 ‘예방/회피/검출 후 회복’이 있다.

교착 상태 예방(Prevention)

앞서 말한 코프만 조건을 하나씩 비틂으로써 교착을 예방할 수 있다. 그놈의 식사하는 철학자 문제(dining philosophers problem) 또 다시 등판.

교착 예방 방법	설명
자원의 상호 배제를 없앰	모든 자원이 공유 가능해지는 것인데, 현실적으로 무리가 있다.
점유와 대기 없앰	프로세스에 필요한 자원을 전부 동시에 얻을 수 있을 때에만 자원을 점유하고, 그렇지 않다면 대기하라는 이야기. 프로세스가 실행되려면 다른 자원들을 몰아줘야 하기에 자원의 활용률이 떨어진다.
비선점 조건 없앰	선점하여 사용할 수 있는 일부 자원에 대해서는 효과적이지만, 선점 불가능한 자원들도 얼마든지 있기에 범용성이 떨어진다.
원형 대기 조건 없앰	모든 자원에 번호를 붙이고, 오름차순으로 자원을 할당한다. 그러나 실제 자원들에 일일이 번호를 붙이는 것은 간단하지 않고, 번호 순서에 따라 자원의 활용률이 떨어질 수 있다.

자 이 원형 대기(circular wait)에서 내가 4~5시간이나 구글링도 하고 유튜브도 찾고 코드도 만지고 별 쌩일을 다했다. (다 피가 되고 살이 되겠지…)

일단 책 379페이지의 원형 사이클이 이해가 안된다. 분명 오름차순으로 자원을 할당받기에 5번 포크는 최상단의 철학자에게 할당되지 않고, 그 이전 철학자에게 할당될 것이다. 따라서 화살표 방향이 바뀌어야할 것 같은데, 이건 질문으로 남겨놓겠다. (Q) 나중에 내가 답변할 수 있기를

(★) 순서 매기기를 통한 ‘식사하는 철학자 문제’ 해결(Ordering of Resources/Resource Hierarchy Solution)

도저히 이 순서 매기기를 통한 해결법이 이해가 안되더라. 뭐 홀수(odd)번째는 왼쪽을 짝수(even)번째는 오른쪽을 먼저 집는다든지, 최대 4명만 앉을 수 있게 한다든지, 여러 해결책을 보았다. 하지만 순서 매기는 걸로는 어떻게 하는지 모르겠어서 상당히 해맸다.

내가 일단 내린 결론은, 앞서 말한 ‘책의 도식’에 오류가 있다!는 주장이다. 화살표가 저 방향일 수가 없다.

관련한 문서들의 설명들을 정말 많이 찾아봤는데, 그나마 내 마음에 와닿은 두 문서 링크를 걸어 놓는다.

가장 큰 도움이 된 인도 분의 (역시 믿습니다.. 인멘..) 영상도 걸어 둔다.

핵심은, 1. 양쪽 중 더 작은 번호의 포크를 집을 수 없다면 해당 철학자는 가만히 생각만 한다 / 2. 양쪽 포크를 집어 식사를 한다면 다음 턴이 되어 포크를 반드시 내려놓는다. / 3. 1번 철학자부터 N번 철학자의 순서로 각 한 턴씩만 제공한 채 돌아간다 / 이렇게 3가지 가정하에, 항상 1번과 N번 철학자는 나머지 철학자들의 반 밖에 먹지 못한다라는 것이다.

왜 그런 판단을 내렸냐고? 먼저 내가 작성한 C++ 코드부터 소개한다.

/* Code by Partial02!!!!!!
To impose a linear ordering on the semaphores.
This order could be imposed by requiring i < j anytime sems[i] is accessed before sems[j].
As before, thread 1 would wait on semaphores 0 and 1 (in that order),
thread 2 would wait on semaphores 1 and 2, and so on.
However, the last thread would have a different ordering.
If there are N semaphores (numbered 0 through N-1), the last thread would have to wait on semaphore 0
before semaphore N-1 to adhere to the linear ordering. */

#include <iostream>
int arrayFork[5]; // Fork 0 ~ 4
int arrayPhilo[5]; // Counting Philosophers' dining
bool sem_lock(int p); // semaphores for the forks
void verifyPhilo(int p); // check whether the philosopher dines
using namespace std;

int main(void)
{
    for (int i = 0; i < 100; i++) {
        if (sem_lock(i % 5 + 1))
            verifyPhilo(i % 5 + 1);
        // If philosopher(i % 5 + 1) successfully pick the fork up, check whether philosopher dines
    }
    
    for (int j = 0; j < 5; j++) cout << "P" << j + 1 << " dines " << arrayPhilo[j] << " times\n";
    return 0;
}
bool sem_lock(int p) // true when the semaphore locked
{
    int l = p - 1;
    int r = p < 5 ? p : 0;  // Philo1 ~ Philo4 vs. Philo5
    int s = l < r ? l : r; // smaller one
    int b = l < r ? r : l; // bigger one
    
    if (arrayFork[s] == 0) {
        arrayFork[s] = p;
        return true;
    }
    else if (arrayFork[s] == p) { // If philoP owns fork s
        if (arrayFork[b] == 0) {
            arrayFork[b] = p;
            return true;
        }
        else if (arrayFork[s] == arrayFork[b]) { // the philosopher finished dining
            arrayFork[s] = 0; // unlock the semaphore
            arrayFork[b] = 0;
            return false;
        }
        else return false; // two forks have different owner
    }
    return false; // philoP doesn't own fork s, blocked.
}
void verifyPhilo(int p)
{
    int l = p - 1;
    int r = p < 5 ? p : 0;  // Philo1 ~ Philo4 vs. Philo5
    if (arrayFork[l] == arrayFork[r]) {
        cout << "PHILOSOPHER " << p << " DINES!\n";
        arrayPhilo[p - 1] += 1;
    }
}

이 코드를 실행한 결과는 다음과 같다.

PHILOSOPHER 4 DINES!
PHILOSOPHER 3 DINES! // 3번 철학자로부터 주기의 절반이 시작된다.
PHILOSOPHER 2 DINES!
PHILOSOPHER 4 DINES!
PHILOSOPHER 1 DINES! // 3-2-4-1의 주기 절반. 1번 철학자의 식사는 나머지의 절반에 수렴한다.
PHILOSOPHER 3 DINES! // 다시 3번 철학자로부터 주기의 절반이 시작된다.
PHILOSOPHER 2 DINES!
PHILOSOPHER 4 DINES!
PHILOSOPHER 5 DINES! // 최대의 피해자인 5번 철학자. 역시 3-2-4-5의 주기 절반이 돌아왔다.
PHILOSOPHER 3 DINES! // 다시 주기 시작
PHILOSOPHER 2 DINES!
PHILOSOPHER 4 DINES!
PHILOSOPHER 1 DINES!
PHILOSOPHER 3 DINES!
PHILOSOPHER 2 DINES!
PHILOSOPHER 4 DINES!
PHILOSOPHER 5 DINES!
PHILOSOPHER 3 DINES!
P1 dines 2 times // 1번 철학자는 전체의 절반밖에 식사 기회가 없었다.
P2 dines 4 times
P3 dines 5 times
P4 dines 5 times
P5 dines 2 times // 최대 피해자인 5번 철학자도 역시 반밖에 못 먹는다.

보다시피 1번과 마지막 철학자가 가장 피해를 보는 알고리즘이다.

그런데 여기서 철학자와 포크의 수 N을 일반화해서 나타내보니 다음과 같이 신기한 결과가 나온다.

ordering_resoures

주기 절반이 일반화될 거라고는 생각했는데, 주기의 시작점인 3번 철학자가 첫 식사를 하기 전의 사람 수를 세어본 Gn도 일반화가 되었다. 뭐지? 이거 논문감 아닌가? 뭔가 내가 새로운 걸 발견한 것 같아 뿌듯하다. 어째서 이런 규칙이 생기는 걸까? 또 조건을 바꾸면 어떻게 일반식이 변화하고, 어떻게 이 식을 적용할 수 있을까? 무튼 신기할 따름

아 반복문의 반복 횟수를 무한히 늘리면, 상술했듯 1번과 N번 철학자의 식사 확률은 나머지의 절반에 수렴하게 되는 것도 보일 수 있다. 즉 이 방법을 쓰면 교착은 없더라도 기아(starvation)가 발생하는 것

교착 상태 회피(Avoidance)

이번엔 교착 상태가 발생하지 않을 정도로만 조심히 자원을 할당해 보자. 교착이 발생할 가능성이 있긴 하더라도, 아무튼간에 교착 상태 없이 안전하게 프로세스들에 자원을 할당할 수 있는 순서가 있다면, 이를 안전 상태(safe state)라 부른다. 이 순서를 안전 순서열(safe sequence)이라고 부르는데, 이 안전 순서열이 존재만 한다면 안전 상태, 아예 존재하지 않는다면 불안전 상태(unsafe state)라 부른다.

책의 예제가 너무 좋아서 그대로 따오자면, 현재 컴퓨터 시스템에 총 12개의 자원이 있고, 프로세스 P1 P2 P3가 각각 5 2 2개의 자원을 할당받아 사용 중이라고 가정하자. 그럼 남은 자원은 3개겠지? 각 프로세스의 최대 요구량이 10 4 9이며, 각 프로세스는 최대 요구량의 자원을 받아야만 실행이 종료된다고 하면

이때 P2 P1 P3는 안전 순서열이된다. (직접 해보면 아주 깔끔하게 떨어진다) 그런데 만약 P3에 원래부터 3만큼의 자원이 할당되어 있었다면 어떻게 해도 교착 상태를 회피할 수가 없어진다.

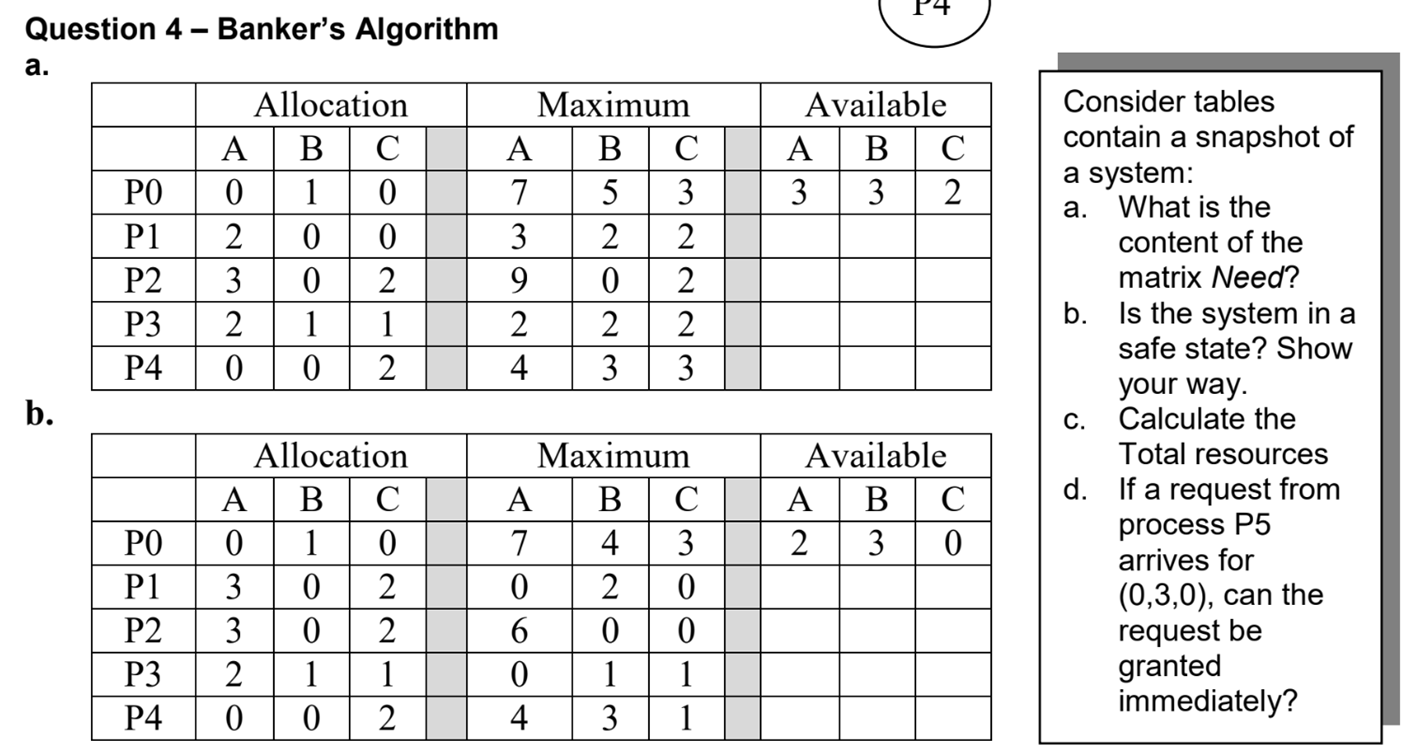
관련해서 은행원 알고리즘(banker’s algorithm)이 있다고 하는데, 오늘은 졸려서 여기까지.. 나중에 기회가 되면 살펴보자.

교착 상태 검출 후 회복(Recovery)

이건 사후 조치이다. 교착이 발생한다면 선점(preemptive)을 통해 프로세스에 자원을 몰아줌으로써 회복시킬 수도 있고, 프로세스를 강제 종료하여 문제 자체를 없애버릴 수도 있다.

이때 모든 프로세스를 동시에 종료시키는 강수를 쓴다면 교착 상태는 단번에 해결되지만 작업 내역을 잃게 되는 문제가 생긴다.

반대로 교착 상태가 없어질 때가지 한 프로세스씩 강제 종료(=자원 회수)한다면 작업 내역을 잃는 프로세스는 최대한 줄일 수 있지만, 오버헤드가 발생하게 된다.

아 참고로, 위의 한 프로세스씩 강제 종료하는 것을 choose deadlock victims한다고 부른다. (한국어로 희생자 선택의 원칙?)

교착 상태 무시(Ignoring)

엥 위에서 3개만 언급했는데 ‘무시’하는 건 또 뭘까? 그냥 교착 상태가 나든 말든 신경 안쓰고 내 갈길 간다는 마인드. (눈가리고 아웅? 이건 아닌가)

흔히 타조 알고리즘(ostrich algorithm)이라고 부르는데, 그냥 그런갑다 하자. 별 뜻 없는 듯.

출처: [혼자 공부하는 컴퓨터구조+운영체제 Chapter 13]

Twitter Facebook LinkedIn